Can you divide a curve using chord distances?

[NickN]

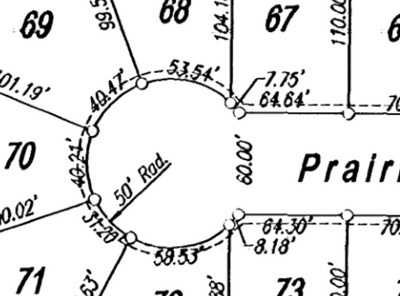
I have a plat with a cul-de-sac where I need to split the curve by the lot lines.

I drew in the cul-de-sac just fine, but the plat specifies that distances shown along curves (including cul-de-sacs) are chord lengths not arc lengths. I tried using units shortcuts in the divide tool but it doesn't seem to recognize them or I was doing it wrong. What's the proper way to do this or do I have to do the conversion to arc lengths myself?

Thanks!

[anna_garrett]

i've never seen that before and i'm sorry they did that! can you not just sketch the curve with the traverse tool using the chord direction & length parameters instead?

[NickN]

Since there's no curve table, just the chord lengths, I don't know the chord bearings of the individual lot frontages along the curve.

I can do the math to convert the chord lengths to arcs and then divide using those values but I just wanted to make sure I wasn't overlooking the proper way to do it.

[anna_garrett]

i genuinely can't think of a way to finagle the divide tool to fit the data you have. 

i would just convert the values.

[jcarlson]

You probably can't do it with the Divide tool, but could you use the Split tool, then use the distance constraint to add your vertices? Still, very manual and tedious, though.

[NickN]

Do you mean drawing the chords with the specified lengths where it intersects the curve then split at those?

[jcarlson]

Yes. When you're sketching the cutline in the Split tool, you can use all the same editing hotkeys and constraints as when you digitize new features.

So when you start drawing a cutline, you could add the first vertix at the beginning of the curve, then press D for "distance", enter the first chord length, add a vertex where that radius meets the curve.

Then just repeat for each chord! Your curve should split right at the vertices. The only problem with this method is that it will shift all of any potential error onto the final segment of the curve. Not perfect, but it works. If there's a significant error, it may be worth converting to arc lengths in order to divide everything proportionately.

[NickN]

Ah yeah, I had tried that and ended up with the situation you described where all the error is in the last segment. Looks like Amir's suggestion below is probably the way to go for this situation. Thanks for your input!

[BillFox]

you could draw in the lot lines (short them) and extend/intersect into your curve

[BillFox]

or, assume tangent curves and calculate your way around from the street bearing using deltas - similar to when they don't give you radial bearings.