- Home
- :
- All Communities
- :
- Industries
- :
- Transportation
- :
- Transportation Questions
- :
- Calculated locations differ from plotted locations
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Calculated locations differ from plotted locations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hello
Please accept my apologies in advance if this proves to be the result of an elementary mistake.
I have a set of observations made from given points. For each of these I have an observer location (coordinates) and a distance (metres) and bearing (degrees) to an observation target. I want to determine the perpendicular distance of this observation target from a specific route(line). When mapped (Projected Coordinate System = British National Grid) the perpendicular distances produced (identified using 'Generate Near Table' and checked roughly using the measurement tool) differ markedly (10-40%), and inconsistently, from those obtained if I calculate the distance from the original data using simple trigonometry. Given that the units of the coordinate system are metres and the distances are not geographically large (generally <500m), I'm struggling to understand why this should be. What am I missing?
The attached document perhaps gives a clearer explanation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Is there any chance that your dataframe (arcmap) or map (ArcGIS Pro) has been tainted with a Web Mercator dataset? (it causes errors in distance and area measurements. Your calculation from the numbers is correct,
np.sin(np.deg2rad(40))*180. = 115.70176974357706 , but where did you get those numbers? from the measure tool or from points representing the triangle itself?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi Dan,
Thanks for getting back to me. I have not used, or re-projected anything to, a Web Mercator dataset on the dataframe (I'm using ArcGIS 10.5). The numbers are from empirical measurements taken in the field using a laser rangefinder (Distance) and old-school compass (Bearing) so there should be no issue with any 'electronic interpretation/adjustment'. Nevertheless, this wouldn't make a difference would it? If I plot some randomly-derived pairs of points on the map (in the same format as the pdf example) and then compare the perpendicular distances between the targets and the line with those derived from trig calculations, there are still discrepancies.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
strange a sample of the data used might help.
when you mention 'old school compass' as in one that references to magnetic north, I remember from student surveying labs them forgetting to adjust for the magnetic declination on the compass or post data collection
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I've attached a package of some data - hopefully I've managed to do this correctly and you can then see what I mean.
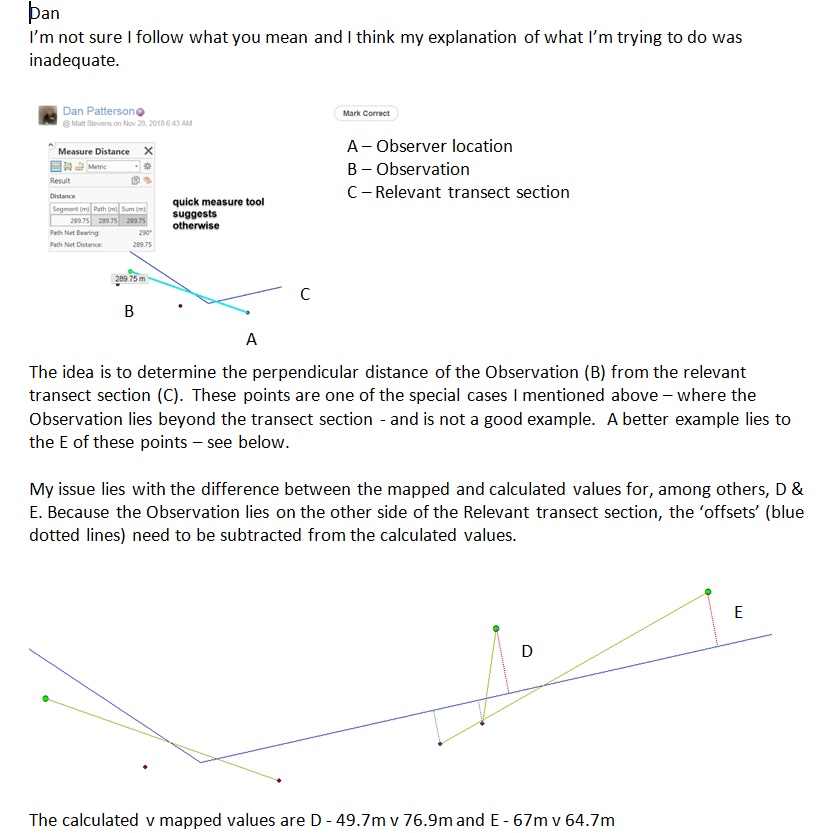
To clarify, the idea is to determine the perpendicular distance from each of the 'KESTRSprCON2016_Location' points to the relevant line (layers with 'TITL' in the name) section. The original 'From' locations are given by the 'c2016SprCON_Project' points and I've included a line between these points to aid identification. Please ignore the other points. Lastly, I am aware that some of the 'Location' points extend beyond the length of the relevant line section, these are a special case and should be ignored for now.
With regard to your point re. magnetic declination, this is of limited relevance here since this is ca.1 degree in the section of map shown here. Also, the error in measurement of bearing by fieldworkers is likely to be greater than this anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Matt
Trying to figure out this example location are the angular units in mils? or did they do a quick twirl around to go past 360 degrees?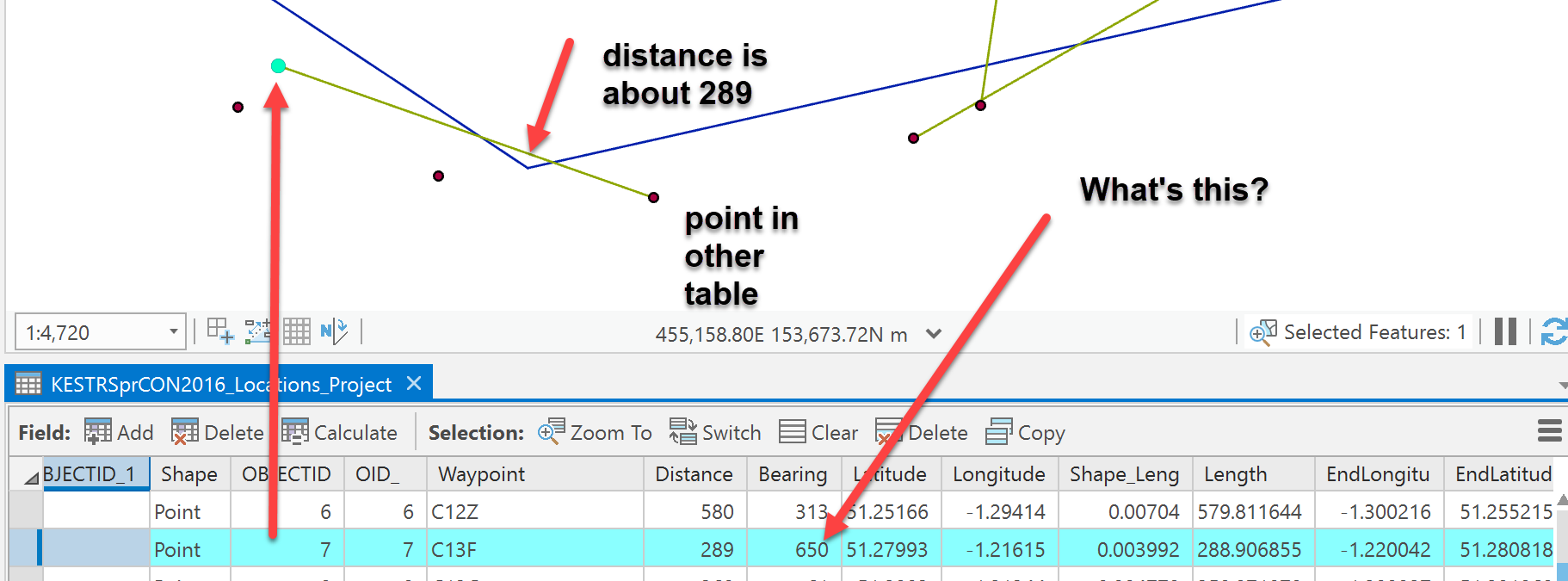
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Dan
Sorry, you've managed to find one of the two errors in the dataset that I forgot to correct before sending:
OID7 - Distance and Bearing are transposed - they should be the other way round - Distance = 650, Bearing 289
OID22 (in c2016SprCON_Project) - Typo. Distance should be 336 and not 3360
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
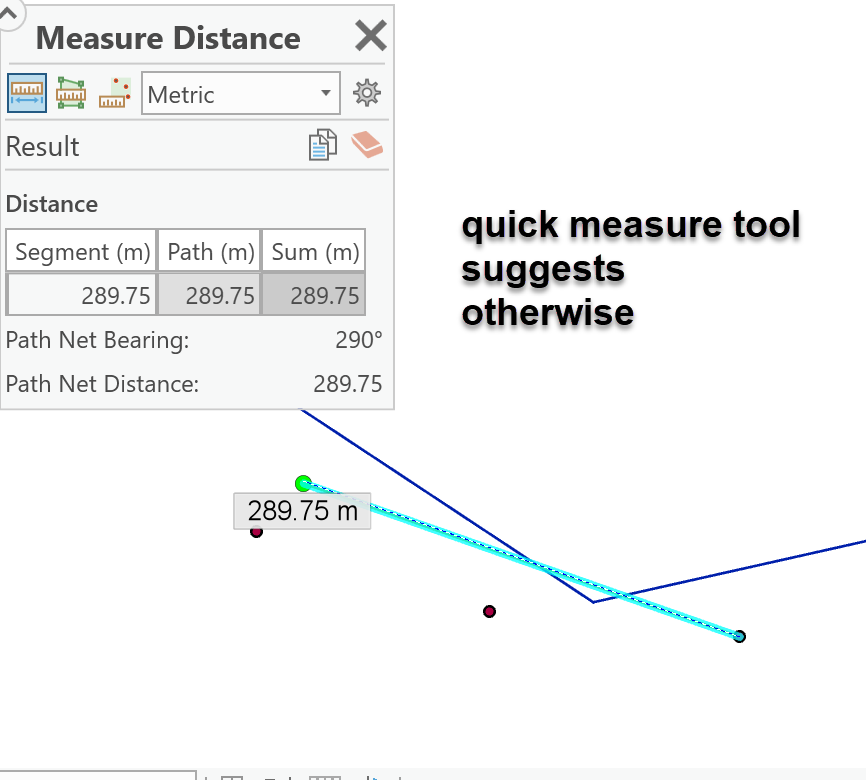
Not in the first case
Perhaps for 7, 8 and 9 , the lines in the first image, can you show what you got for those locations close to the blue line.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Matt, I will check those two examples... I just got stuck on the one on the left, where the distance was 288 (measured and in table) but the bearing was 640.
I will check D and E later