By any other name ... the questions are all the same. They only differ by whether you want the result or its opposite.
The generic questions can be looked from the traditional perspectives of
- what is the question,
- what is the object in the question and
- what are the object properties.
What is the same?
| |
|---|
geometry- points
- X, Y, Z, M and or ID values
- lines
- the above plus
- length
- angle/direction total or by part
- number of points (density per unit)
- parts
- open/closed circuit
- polygons
- the above plus
- perimeter (length)
- number of points
- parts
- holes?
| attributes- numbers
- floating point (single or double precision)
- integer (long or short
- boolean (True or False and other representations)
- text/string
- matching
- contains
- pattern (order, repetition etcetera)
- case (upper, lower, proper, and other forms)
- date-time
|
What to to with them?
| |
|---|
find them- everything...exact duplicates in every regard
- just a few attributes
- just the geometry
- the geometry and the attributes
copy them- to a new file of the same type
- to append to an existing file
- to export to a different file format
delete them- of course... after backup
- just the ones that weren't found (aka... the switch)
| - change them
- alter properties
- geometric changes enhance
- positional changes
- representation change
|
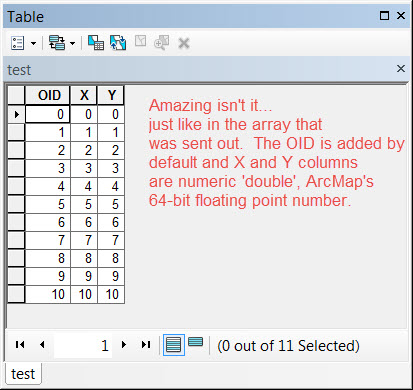
Lets start with a small point data file brought in from Arcmap using the FeatureClassToNumPyArray tool.
Four fields were brought in, the Shape field ( as X and Y values), an integer Group field and a Text field. The data types for each field are indicated in the dtype line. The details of data types have been documented in other documents in the series.
>>> arr
array([(6.0, 0.0, 4, 'a'), (7.0, 9.0, 2, 'c'),
(8.0, 6.0, 1, 'b'), (3.0, 2.0, 4, 'a'),
(6.0, 0.0, 4, 'a'), (2.0, 5.0, 2, 'b'),
(3.0, 2.0, 4, 'a'), (8.0, 6.0, 1, 'b'),
(7.0, 9.0, 2, 'c'), (6.0, 0.0, 4, 'a')],
dtype=[('X', '<f8'), ('Y', '<f8'), ('Group', '<i4'), ('Text', 'S5')])
>>> arr.shape
(10,)
In summary:
- the X and Y fields 64 bit floating point numbers (denoted by: <f8 or float64)
- the Group field is a 32 bit integer field (denoted by: <i4 or int32)
- the text field is just that...a field of string data 5 characters wide.
Is any of this important? Well yes...look at the array above. The shape indicates it has 10 rows but no columns?? Not quite what you were expecting and it appears all jumbled and not nicely organized like a table in ArcMap or in a spreadsheet. The array is a structured array, a subclass of the multidimensional array class, the ndarray. The data types in structured arrays are mixed and NumPy works if the data are of one data type like those in the parent class
Data in an array can be cast to find a common type, if it contains one element belongs to a higher data type. Consider the following examples, which exemplify this phenomenon.
The arrays have been cast into a data type which is possible for all elements. For example, the 2nd array contained a single floating point number and 4 integers and upcasting to floating point is possible. The 3rd example downcast the integers to string and in the 4th example, True was upcast to integer since it has a base class of integer, which is why True-False is often represented by 1-0.
>>> type(True).__base__
<type 'int'>
The following code will be used for further discussion.
def get_unique(arr,by_flds=[]):
""" Produce unique records in an array controlled by a list of fields.
Input: An array, and a list of fields to assess unique.
All fields: Use [] for all fields.
Remove one: all_flds = list(arr_0.dtype.names)
all_flds.remove('ID')
Some fields: by name(s): arr[['X','Y']]
or slices: all_flds[slice]... [:2], [2:], [:-2] [([start:stop:step])
Returns: Unique array of sorted conditions.
The indices where a unique condition is first encountered.
The original array sliced with the sorted indices.
Duh's: Do not forget to exclude an index field or fields where all values are
unique thereby ensuring each record will be unique and you will fail miserably.
"""
a = arr.view(np.recarray)
if by_flds:
a = a[by_flds].copy()
N = arr.shape[0]
if arr.ndim == 1:
uniq,idx = np.unique(a,return_index=True)
uniq = uniq.view(arr.dtype).reshape(-1, 1)
else:
uniq,idx = np.unique(arr.view(a.dtype.descr * arr.shape[1]),return_index=True)
uniq = uniq.view(arr.dtype).reshape(-1, arr.shape[1])
arr_u = arr[np.sort(idx)]
return uniq,idx,arr_u
if __name__=="__main__":
"""Sample data section and runs...see headers"""
X = [6,7,8,3,6,8,3,2,7,9]; Y = [0,9,6,2,0,6,2,5,9,4]
G = [4,2,1,4,3,2,2,3,4,1]; T = ['a','c','b','a','a','b','a','c','d','b']
dt = [('X','f8'),('Y','f8'),('Group','i4'),('Text','|S5')]
arr_0 = np.array(zip(X,Y,G,T),dtype=dt)
uniq_0,idx_0,arr_u0 = get_unique(arr_0[['X','Y']])
frmt = "\narr_0[['X','Y']]...\nInput:\n{}\nOutput:\n{}\nIndices\n{}\nSliced:\n{}"
print(frmt.format(arr_0,uniq_0,idx_0,arr_u0))
Which yields the following results
arr_0[['X','Y']]...
Input:
[(6.0, 0.0, 4, 'a') (7.0, 9.0, 2, 'c') (8.0, 6.0, 1, 'b')
(3.0, 2.0, 4, 'a') (6.0, 0.0, 3, 'a') (8.0, 6.0, 2, 'b')
(3.0, 2.0, 2, 'a') (2.0, 5.0, 3, 'c') (7.0, 9.0, 4, 'd')
(9.0, 4.0, 1, 'b')]
Output:
[[(2.0, 5.0)]
[(3.0, 2.0)]
[(6.0, 0.0)]
[(7.0, 9.0)]
[(8.0, 6.0)]
[(9.0, 4.0)]]
Indices
[7 3 0 1 2 9]
Sliced:
[(6.0, 0.0) (7.0, 9.0) (8.0, 6.0) (3.0, 2.0) (2.0, 5.0)
(9.0, 4.0)]
The arr_0 output is your conventional recarray output with everything wrapped around making it hard to read. The Output section showsn the unique X,Y values in the array in sorted order, which is the default. The Indices output is the location in the original array where the entries in the sorted Output can be found. To produce the Sliced incarnation, I sorted the Indices, then used the sorted indices to slice the rows out of the original array.
Voila...take a table, make it an array...find all the unique entries based upon the whole array, or a column or columns, then slice and dice to get your desired output. In any event, it is possible to terminate the process at any point and just find the unique values in a column for instance.
The next case will show how to deal with ndarrays which consist of a uniform data type and the above example will not work.
Of course there is a workaround. To that end, consider the small def from a series I maintain, that shows how to recast an ndarray with a single dtype to a named structured array and a recarray. Once you have fiddled with the parts, you can
- determine the unique records (aka rows)
- get them in sorted order or
- maintain the original order of the data
def num_42():
"""(num_42)...unique while maintaining order from the original array
:Requires: import numpy as np
:--------
:Notes: see my blog for format posts, there are several
:-----
: format tips
: simple ["f{}".format(i) for i in range(2)]
: ['f0', 'f1']
: padded ["a{:0>{}}".format(i,3) for i in range(5)]
: ['a000', 'a001', 'a002', 'a003', 'a004']
"""
a = np.array([[2, 0], [1, 0], [0, 1], [1, 0], [1, 2], [1, 2]])
shp = a.shape
dt_name = a.dtype.name
flds = ["f{:0>{}}".format(i,2) for i in range(shp[1])]
dt = [(fld, dt_name) for fld in flds]
b = a.view(dtype=dt).squeeze()
c, idx = np.unique(b, return_index=True)
d = b[idx]
return a, b, c, idx, d
The results are pretty well as expected.
- Array 'a' has a uniform dtype.
- The shape and dtype name were used to produce a set of field names (see flds and dt construction).
- Once the dtype was constructed, a structured or recarray can be created ( 'b' as structured array).
- The unique values in array 'b' are returned in sorted order ( array 'c', see line 21)
- The indices of the first occurrence of the unique values are also returned (indices, idx, see line 21)
- The input structured array, 'b', was then sliced using the indices obtained.
>>> a
array([[2, 0],
[1, 0],
[0, 1],
[1, 0],
[1, 2],
[1, 2]])
>>> b
array([(2, 0), (1, 0), (0, 1), (1, 0), (1, 2), (1, 2)],
dtype=[('f00', '<i8'), ('f01', '<i8')])
>>> c
array([(0, 1), (1, 0), (1, 2), (2, 0)],
dtype=[('f00', '<i8'), ('f01', '<i8')])
>>> idx
array([2, 1, 4, 0])
>>> d
array([(0, 1), (1, 0), (1, 2), (2, 0)],
dtype=[('f00', '<i8'), ('f01', '<i8')])
>>>
>>> idx_2 = np.sort(idx)
>>> idx_2
array([0, 1, 2, 4])
>>> b[idx_2]
array([(2, 0), (1, 0), (0, 1), (1, 2)],
dtype=[('f00', '<i8'), ('f01', '<i8')])
I am sure a few of you (ok, maybe one), is saying 'but the original array was a Nx2 array with a uniform dtype? Well I will leave the solution for you to ponder. Once you understand it, you will see that it isn't that difficult and you only need a few bits of information... the original array 'a' dtype, and shape and the unique array's shape...
>>> e = d.view(dtype=a.dtype).reshape(d.shape[0],a.shape[1])
>>> e
array([[0, 1],
[1, 0],
[1, 2],
[2, 0]])
These simple examples can be upcaled quite a bit in terms of the number of row and columns and which ones you need to participate in the uniqueness quest.
That's all for now.