- Home
- :
- All Communities
- :
- Developers
- :
- Native Maps SDKs
- :
- .NET Maps SDK Questions
- :
- How to calculate/get 4 points (and angle) of a rec...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to calculate/get 4 points (and angle) of a rectangle by two corners
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi guys,
I'm kinda lost with my problem after hours of reading and research so I hope you can help!
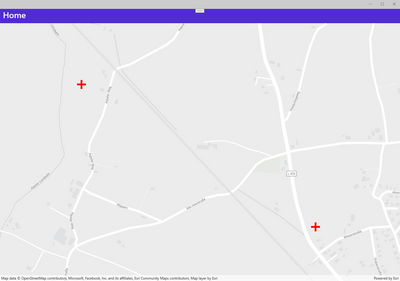
I have two points (red) on a map like this:
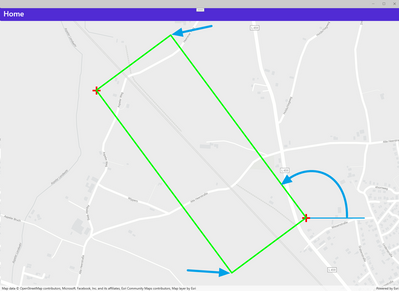
And I like to calculate the two other points and angle in degrees of the rectangle (blue arrows) for a given aspect ratio of the rectangle:
I do not need to draw them on a map, just calculation and just in 2D Cartesian mathematics.
I've looked through all the GeometryEngine methods and couldn't find anything I can do a rotation of a Polyline for example...
It may be possible to do it with Extend and Intersections (also mentioned here) once I can draw the green rectangle... but its kinda complicated.
Anyhow: How do I get/draw the four sides of this rectangle?
Also MultipointBuilder looks promising... but can it draw a rectangle?
Finally reading through geometry help and make-measurements didn't really help. Although it mentions AngularUnits it does not say how to determine an angle of a Polyline or Segment.
Thanks for your help!
Soko
PS: Am I overthinking this to much in a big way? Can I do the calculations with simple trigonometry instead of GeoemtryEngine methods?
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Am I overthinking this to much in a big way? Can I do the calculations with simple trigonometry instead of GeoemtryEngine methods?
Probably. I don't know anything about the .Net SDK, but here is what you could do in pure Python (without using the arcpy geometry methods):
import math
# some basic trigonometry functions
# points as coordinate tuples
# angles in radians
def distance(p1, p2):
return math.sqrt(math.pow(p1[0] - p2[0], 2) + math.pow(p1[1] - p2[1], 2))
def angle(p1, p2):
return math.atan2(p2[1] - p1[1], p2[0] - p1[0])
def point_from_angle_and_distance(p, a, d):
return (p[0] + d * math.cos(a), p[1] + d * math.sin(a))
def get_rectangle(p1, p2, aspect):
""" Outputs the vertices of the (a) rectangle defined by the two given corner points and the aspect ratio.
p1, p2: Coordinate tuples of two points in a diagonal of the rectangle
aspect: ratio of the two sites (<= 1)
"""
# get the center of the diagonal
a_p1p2 = angle(p1, p2)
d_p1p2 = distance(p1, p2)
center = point_from_angle_and_distance(p1, a_p1p2, d_p1p2 / 2)
# convert the aspect ratio to angle between the diagonals
a_diag = math.pi - 2 * math.atan(aspect)
# get the other two points
p3 = point_from_angle_and_distance(center, a_p1p2 - a_diag, d_p1p2 / 2)
p4 = point_from_angle_and_distance(center, a_p1p2 + math.pi - a_diag, d_p1p2 / 2)
# reorder and return
return [p1, p3, p2, p4]
Now let's give that method a spin... We will read from a Multipoint layer, convert the multipoints to coordinate tuples, calculate the resulting rectangle for multiple aspect ratios, convert those rectangles into arcpy.Polygons and write them into a polygon layer.
aspect_ratios = [0.01, 0.25, 0.5, 0.75, 1]
with arcpy.da.InsertCursor("TestPolygons", ["SHAPE@", "DoubleField1"]) as i_cursor:
with arcpy.da.SearchCursor("TestMultipoints", ["SHAPE@"]) as s_cursor:
for shp, in s_cursor:
p1 = (shp.firstPoint.X, shp.firstPoint.Y)
p2 = (shp.lastPoint.X, shp.lastPoint.Y)
for aspect in aspect_ratios:
rect_points = get_rectangle(p1, p2, aspect)
vertices = [arcpy.Point(p[0], p[1]) for p in rect_points]
poly = arcpy.Polygon(arcpy.Array(vertices), spatial_reference=arcpy.SpatialReference(25833))
i_cursor.insertRow([poly, aspect])
Result:
So yeah, you just need basic trigonometry for this.
Have a great day!
Johannes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Am I overthinking this to much in a big way? Can I do the calculations with simple trigonometry instead of GeoemtryEngine methods?
Probably. I don't know anything about the .Net SDK, but here is what you could do in pure Python (without using the arcpy geometry methods):
import math
# some basic trigonometry functions
# points as coordinate tuples
# angles in radians
def distance(p1, p2):
return math.sqrt(math.pow(p1[0] - p2[0], 2) + math.pow(p1[1] - p2[1], 2))
def angle(p1, p2):
return math.atan2(p2[1] - p1[1], p2[0] - p1[0])
def point_from_angle_and_distance(p, a, d):
return (p[0] + d * math.cos(a), p[1] + d * math.sin(a))
def get_rectangle(p1, p2, aspect):
""" Outputs the vertices of the (a) rectangle defined by the two given corner points and the aspect ratio.
p1, p2: Coordinate tuples of two points in a diagonal of the rectangle
aspect: ratio of the two sites (<= 1)
"""
# get the center of the diagonal
a_p1p2 = angle(p1, p2)
d_p1p2 = distance(p1, p2)
center = point_from_angle_and_distance(p1, a_p1p2, d_p1p2 / 2)
# convert the aspect ratio to angle between the diagonals
a_diag = math.pi - 2 * math.atan(aspect)
# get the other two points
p3 = point_from_angle_and_distance(center, a_p1p2 - a_diag, d_p1p2 / 2)
p4 = point_from_angle_and_distance(center, a_p1p2 + math.pi - a_diag, d_p1p2 / 2)
# reorder and return
return [p1, p3, p2, p4]
Now let's give that method a spin... We will read from a Multipoint layer, convert the multipoints to coordinate tuples, calculate the resulting rectangle for multiple aspect ratios, convert those rectangles into arcpy.Polygons and write them into a polygon layer.
aspect_ratios = [0.01, 0.25, 0.5, 0.75, 1]
with arcpy.da.InsertCursor("TestPolygons", ["SHAPE@", "DoubleField1"]) as i_cursor:
with arcpy.da.SearchCursor("TestMultipoints", ["SHAPE@"]) as s_cursor:
for shp, in s_cursor:
p1 = (shp.firstPoint.X, shp.firstPoint.Y)
p2 = (shp.lastPoint.X, shp.lastPoint.Y)
for aspect in aspect_ratios:
rect_points = get_rectangle(p1, p2, aspect)
vertices = [arcpy.Point(p[0], p[1]) for p in rect_points]
poly = arcpy.Polygon(arcpy.Array(vertices), spatial_reference=arcpy.SpatialReference(25833))
i_cursor.insertRow([poly, aspect])
Result:
So yeah, you just need basic trigonometry for this.
Have a great day!
Johannes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
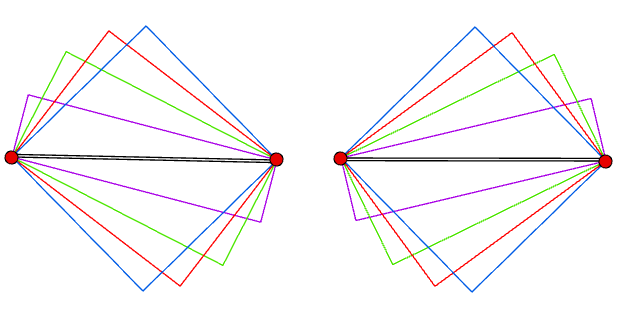
PS: This problem has two solutions, depending on which diagonal the two point describe. If you change line 26 to take the arctan of 1/aspect, you get the second solution.
Left: solution 1 -> atan(aspect), Right: solution 2 -> atan(1/aspect)
Have a great day!
Johannes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi Johannes,
and thanks for the great explanation and phyton code. I'll give it a try to port it to C#.
About the two solutions: The two points are always lower-left, upper-right. So solution 1 is the right one for me.
One thing though I'm worried about:
This pure trigonometry solution works for sure in a "standard" coordinate system. By "standard" I mean were X and Y distances/units are the same.
But longitude and latitute distances are not the same afaik. Apparently even one unit/degree is a different distance depending where you are on the globe.
Do you think this matters?
Soko
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Oh right. this calculation is for cartesian coordinate systems, as per your question.
I have only worked with projected coordinate systems until now, so I'm not really sure how this will play out in a geographical coordinate system. The error might be negligible over small distances, but for greater distances, it will probably become apparent.
Maybe you can get away with converting the points into a locally applicable projected coordinate system, do the calculation, and then project the resulting points into the geographic system.
Have a great day!
Johannes