How to calculate the angle of a line respect to the North
Hi,
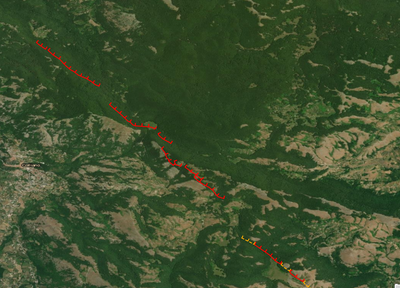
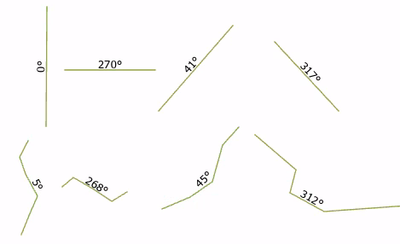
I would like to calculate the angle of the lines in the image respect to the North. Is there a tool that can do that? and eventually put the output in the Attributes table. I know that these lines aren't perfectly straight but I need the average
I'm using ArcGis Pro 3.0.0
Thanks!
Accepted Solutions
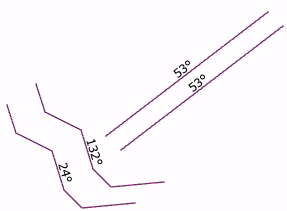
Indeed, the angle is dependent on the vertex order:
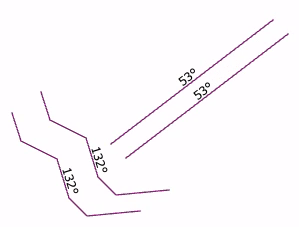
Removing that dependency is easy, but it wasn't quite as trivial as I thought. I thought I just had to replace the modulo 360 with modulo 180 (last line). That works for lines with a single segment, but polylines are still wrong:
Instead, you have to convert to geographic angle inside the loop, not at the end:
// get a list of line parts
var paths = Geometry($feature).paths
// for each part, loop through each segment and get its geographic angle
var angles = []
for(var p in paths) {
var count_p = Count(paths[p])
for(var q = 1; q < count_p; q ++) {
var a_arith = Angle(paths[p][q], paths[p][q-1])
var a_geo = (450 - a_arith) % 180 // 180 instead of 360, so that vertex order doesn't matter
Push(angles, a_geo)
}
}
// return the mean
return Mean(angles)
I don't think there is a tool that does that out of the box (edit: nevermind, see above). But you can easily calculate the value with Calculate Field.
angle of the lines in the image respect to the North
Do you mean the geographic angle (North=0°, East=90°)? If so, use this Arcade expression in the tool:
// get a list of line parts
var paths = Geometry($feature).paths
// for each part, loop through each segment and get its angle (arithmetic angle -> East=0°, North=90°)
var angles = []
for(var p in paths) {
var count_p = Count(paths[p])
for(var q = 1; q < count_p; q ++) {
var a = Angle(paths[p][q], paths[p][q-1])
Push(angles, a)
}
}
// get the mean arithmetic angle
var arith_angle = Mean(angles)
// convert to geographic and return
return (450 - arith_angle) % 360
Or do you mean the arithmetic angle (rotating counter-clockwise) but with North = 0°? Then use this expression:
// get a list of line parts
var paths = Geometry($feature).paths
// for each part, loop through each segment and get its angle (arithmetic angle -> East=0°, North=90°)
var angles = []
for(var p in paths) {
var count_p = Count(paths[p])
for(var q = 1; q < count_p; q ++) {
var a = Angle(paths[p][q], paths[p][q-1])
Push(angles, a)
}
}
// get the mean arithmetic angle
var arith_angle = Mean(angles)
// rotate so that North = 0°
var north_arith_angle = arith_angle - 90
return north_arith_angle + IIF(north_arith_angle < 0, 180, 0)
Or do you mean something else? Then please clarify.
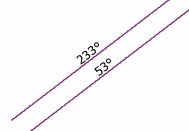
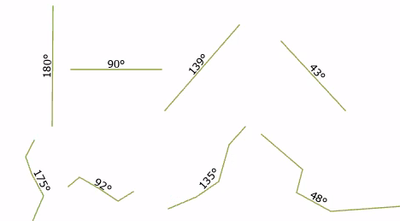
Thank you! I'm indeed calculating the geographic angle and your solution works well, but just in some cases it is odd. For example, for the lines in the image below the dashed line's angle results to be 177° and the one for the solid line is 354°, so they are both wrong... could it be due to the sense in which I drew the lines?
They should be : dashed line around 100° and solid line around 75°
Thanks
Indeed, the angle is dependent on the vertex order:
Removing that dependency is easy, but it wasn't quite as trivial as I thought. I thought I just had to replace the modulo 360 with modulo 180 (last line). That works for lines with a single segment, but polylines are still wrong:
Instead, you have to convert to geographic angle inside the loop, not at the end:
// get a list of line parts
var paths = Geometry($feature).paths
// for each part, loop through each segment and get its geographic angle
var angles = []
for(var p in paths) {
var count_p = Count(paths[p])
for(var q = 1; q < count_p; q ++) {
var a_arith = Angle(paths[p][q], paths[p][q-1])
var a_geo = (450 - a_arith) % 180 // 180 instead of 360, so that vertex order doesn't matter
Push(angles, a_geo)
}
}
// return the mean
return Mean(angles)
