- Home
- :
- All Communities
- :
- Products
- :
- Geoprocessing
- :
- Geoprocessing Questions
- :
- Can you taper a buffer?
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I am looking at creating a tapered buffer for a drain off a field that meets up with the drain that runs alongside the road. the buffer would be used to negotiate with the farmer to create a grassed runway(drain) to minimize erosion of his field. Any help, advice or suggestions is greatly appreciated.
The Pink lines represent the stream delineation that I've run in the area. What I want to do is create a tapered buffer from a point on the pink line(NW-SE) (ex. 15m) from the ditch (E-W pink). We would like to use the teal line(road allowance) to determine how much land creating this buffer the farmer will 'lose' from production.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
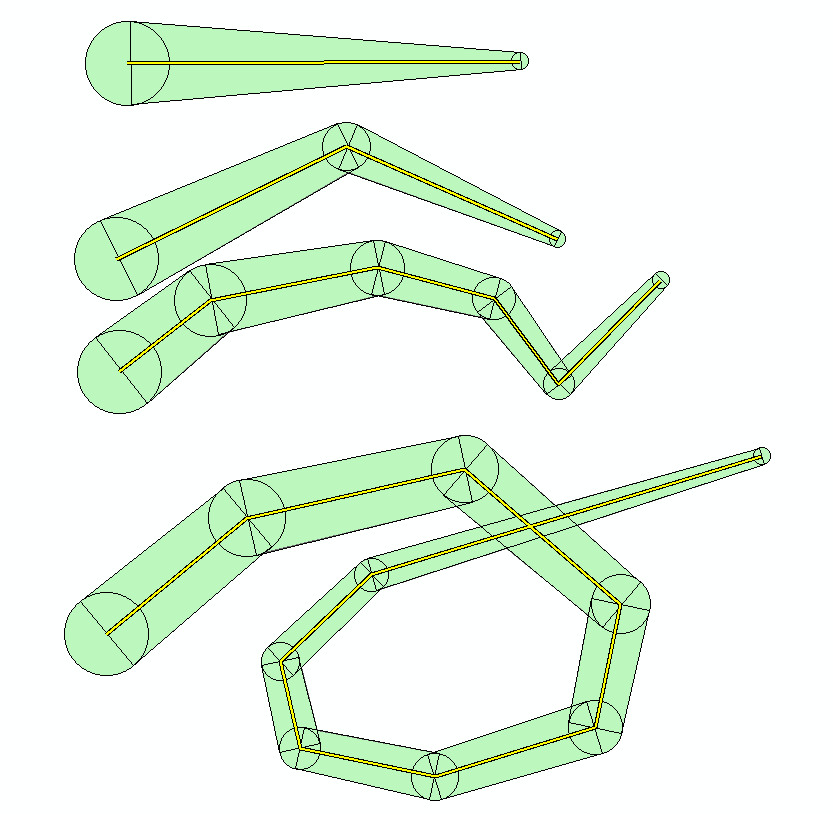
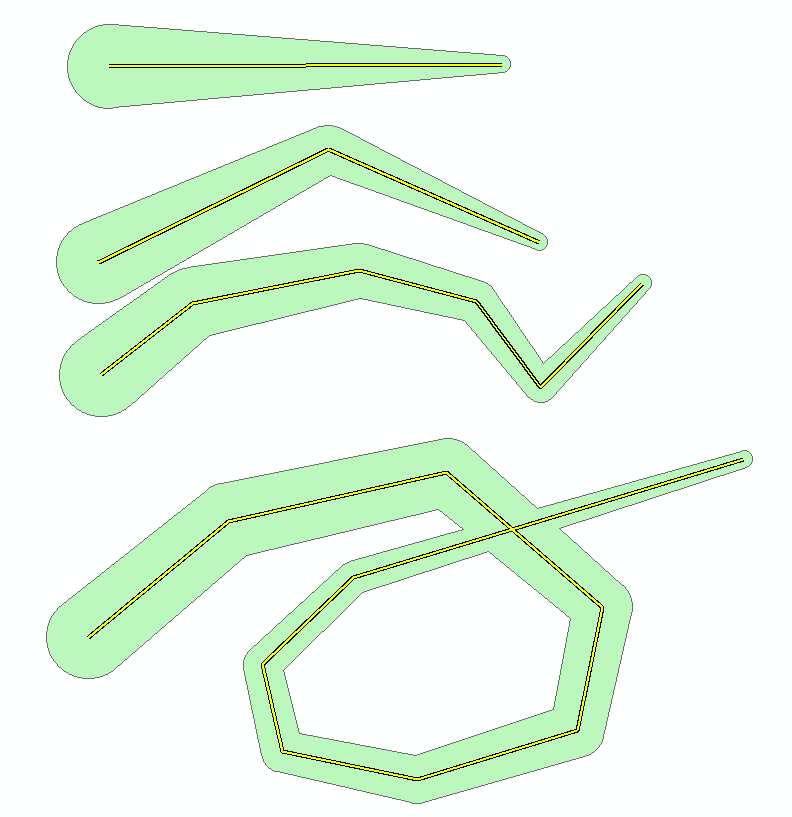
I assume the link in Dan's link is more polished than this, but it caught my interest, and here's the Python code I came up with. Basically, it creates vertex-dependent buffers and trapezoids between the buffers. Math for calculating tangent lines to buffers from here:
>>> lines = 'a_line' # line feature class ... sr = arcpy.Describe(lines).spatialReference # spatial reference ... new_polys = [] ... new_scratch_polys = [] ... new_lines = [] ... buffers = [] ... max_buff = 50 # buffer at line start ... min_buff = 10 # buffer at line end ... with arcpy.da.SearchCursor(lines,'SHAPE@',spatial_reference=sr) as cursor: # loop through lines ... for row in cursor: ... prev_buff = None ... for part in row[0]: ... for pnt in part: ... cur_rad = ((max_buff-min_buff) * (1-row[0].measureOnLine(pnt,True))) + min_buff # calc current proportional buffer size ... cur_buff = arcpy.PointGeometry(pnt,sr).buffer(cur_rad) # create buffer geometry ... new_poly_array = arcpy.Array() ... if prev_buff: # if at least second vertex ... cur_poly = cur_poly.union(cur_buff) # add buffer to cumulative geometry ... c1 = prev_pnt # math starts here. See: Tangent lines to circles ... c2 = pnt ... r1 = prev_rad ... r2 = cur_rad ... dx = c2.X - c1.X ... dy = c2.Y - c1.Y ... dr = r2 - r1 ... d = math.sqrt(math.pow(dx,2)+math.pow(dy,2)) ... X = dx/d ... Y = dy/d ... R = dr/d ... ks = [1,-1] ... for k in ks: ... a = (R*X)-((k*Y)*math.sqrt(1-math.pow(R,2))) ... b = -((R*Y)+((k*X)*math.sqrt(1-math.pow(R,2)))) ... c = r1 - (a*c1.X) + (b*c1.Y) ... tan_x1 = c2.X-10000 ... tan_x2 = c2.X+10000 ... tan_y1 = -((((-a)*(tan_x1))-c)/(b)) ... tan_y2 = -((((-a)*(tan_x2))-c)/(b)) ... new_line = arcpy.Polyline(arcpy.Array([[arcpy.Point(tan_x1,tan_y1),arcpy.Point(tan_x2,tan_y2)]]),sr) # create line ... new_lines.append(new_line) ... if k > 0: ... new_poly_array.add(new_line.intersect(prev_buff,1).centroid) # find intersections ... new_poly_array.add(new_line.intersect(cur_buff,1).centroid) # find intersections ... else: ... new_poly_array.add(new_line.intersect(cur_buff,1).centroid) # find intersections ... new_poly_array.add(new_line.intersect(prev_buff,1).centroid) # find intersections ... new_rect = arcpy.Polygon(new_poly_array,sr) # make polygon from intersections ... new_scratch_polys.append(new_rect) # add rectangle to scratch geometry ... cur_poly = cur_poly.union(new_rect) # add rectangle to cumulative geometry ... else: ... cur_poly = cur_buff # add buffer to cumulative geometry ... prev_rad = cur_rad #remember values ... prev_pnt = pnt ... prev_buff = cur_buff ... buffers.append(prev_buff) ... new_polys.append(cur_poly) # add cumulative geometry to list ... arcpy.CopyFeatures_management(buffers,r'in_memory\buffers') # write outputs ... arcpy.CopyFeatures_management(new_scratch_polys,r'in_memory\scratch_polys') ... arcpy.CopyFeatures_management(new_lines,r'in_memory\lines') ... arcpy.CopyFeatures_management(new_polys,r'in_memory\polys')
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
not much movement since the last time you asked, but I did fine this http://www.arcgis.com/home/item.html?id=cd40be82edb74da78fcf1c0ad07f3e11
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I assume the link in Dan's link is more polished than this, but it caught my interest, and here's the Python code I came up with. Basically, it creates vertex-dependent buffers and trapezoids between the buffers. Math for calculating tangent lines to buffers from here:
>>> lines = 'a_line' # line feature class ... sr = arcpy.Describe(lines).spatialReference # spatial reference ... new_polys = [] ... new_scratch_polys = [] ... new_lines = [] ... buffers = [] ... max_buff = 50 # buffer at line start ... min_buff = 10 # buffer at line end ... with arcpy.da.SearchCursor(lines,'SHAPE@',spatial_reference=sr) as cursor: # loop through lines ... for row in cursor: ... prev_buff = None ... for part in row[0]: ... for pnt in part: ... cur_rad = ((max_buff-min_buff) * (1-row[0].measureOnLine(pnt,True))) + min_buff # calc current proportional buffer size ... cur_buff = arcpy.PointGeometry(pnt,sr).buffer(cur_rad) # create buffer geometry ... new_poly_array = arcpy.Array() ... if prev_buff: # if at least second vertex ... cur_poly = cur_poly.union(cur_buff) # add buffer to cumulative geometry ... c1 = prev_pnt # math starts here. See: Tangent lines to circles ... c2 = pnt ... r1 = prev_rad ... r2 = cur_rad ... dx = c2.X - c1.X ... dy = c2.Y - c1.Y ... dr = r2 - r1 ... d = math.sqrt(math.pow(dx,2)+math.pow(dy,2)) ... X = dx/d ... Y = dy/d ... R = dr/d ... ks = [1,-1] ... for k in ks: ... a = (R*X)-((k*Y)*math.sqrt(1-math.pow(R,2))) ... b = -((R*Y)+((k*X)*math.sqrt(1-math.pow(R,2)))) ... c = r1 - (a*c1.X) + (b*c1.Y) ... tan_x1 = c2.X-10000 ... tan_x2 = c2.X+10000 ... tan_y1 = -((((-a)*(tan_x1))-c)/(b)) ... tan_y2 = -((((-a)*(tan_x2))-c)/(b)) ... new_line = arcpy.Polyline(arcpy.Array([[arcpy.Point(tan_x1,tan_y1),arcpy.Point(tan_x2,tan_y2)]]),sr) # create line ... new_lines.append(new_line) ... if k > 0: ... new_poly_array.add(new_line.intersect(prev_buff,1).centroid) # find intersections ... new_poly_array.add(new_line.intersect(cur_buff,1).centroid) # find intersections ... else: ... new_poly_array.add(new_line.intersect(cur_buff,1).centroid) # find intersections ... new_poly_array.add(new_line.intersect(prev_buff,1).centroid) # find intersections ... new_rect = arcpy.Polygon(new_poly_array,sr) # make polygon from intersections ... new_scratch_polys.append(new_rect) # add rectangle to scratch geometry ... cur_poly = cur_poly.union(new_rect) # add rectangle to cumulative geometry ... else: ... cur_poly = cur_buff # add buffer to cumulative geometry ... prev_rad = cur_rad #remember values ... prev_pnt = pnt ... prev_buff = cur_buff ... buffers.append(prev_buff) ... new_polys.append(cur_poly) # add cumulative geometry to list ... arcpy.CopyFeatures_management(buffers,r'in_memory\buffers') # write outputs ... arcpy.CopyFeatures_management(new_scratch_polys,r'in_memory\scratch_polys') ... arcpy.CopyFeatures_management(new_lines,r'in_memory\lines') ... arcpy.CopyFeatures_management(new_polys,r'in_memory\polys')


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
That is nice Darren!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Thanks Guys this is exactly what I was looking for!
p.s. my posting a second time was just a way to try a catch a different audience.
