- Home
- :
- All Communities
- :
- Products
- :
- Data Management
- :
- Data Management Questions
- :
- Re: Filtering similar point elevations
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Filtering similar point elevations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Created multiple polylines that I identified with the field "Poly_ID"
- Densified the vertices to a 10-foot spacing
- Interpolated the polylines on a DEM raster (3-foot cell resolution)
- Converted the polylines to points
- Created fields "Poly_ID", "X", "Y", and "Z"
- Calculated values for "X", "Y", and "Z"
Goal: Let's say the average number of points for each unique "Poly_ID" is above 1000 but I need to trim it to 500 points.
Question: Aside from starting over with the generalized set of polylines, what process(es) should I utilize that helps me trim the number of points down such that if I were to plot the points before trimming and after trimming on a profile, the differences would be minimal?
An example of this in HEC-RAS, a non-GIS environment, where you can copy and paste cross-section stationing and elevation, go into tool called "Cross-Section Point Filter" and have the program maintain the integrity of your profile while reducing relatively redundant points.
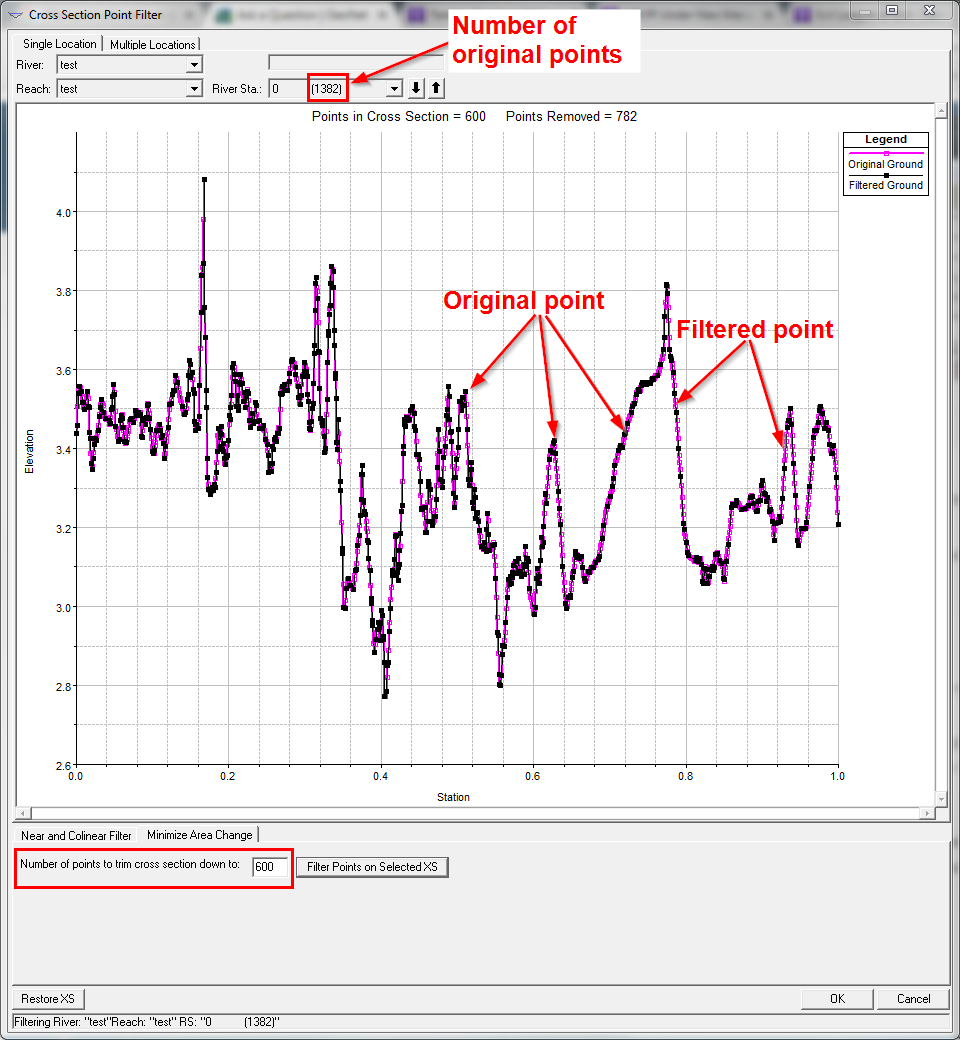
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
you could filter by sequential differences in the values. I can give you an example using python/numpy to illustrate what I mean.
Filter the values in a sequential list of data, retaining only those values where the sequential difference is >= 0.2
>>> a
array([ 1.0, 1.1, 2.0, 2.1, 2.2, 3.0, 5.0, 10.0])
>>> np.ediff1d(a, to_begin=1) > 0.2
array([1, 0, 1, 0, 0, 1, 1, 1], dtype=bool)
>>> a[np.ediff1d(a, to_begin=1) > 0.2]
array([ 1.0, 2.0, 3.0, 5.0, 10.0])
In the above example, a list of values is expressed as an array, a
the sequential 1D differences in the array are determined and compared to a threshold value, 0.2
in the above example, I wanted to retain the first point so I set the to_begin to equal 1 (True in boolean world).
In line 5, the values are extracted (sliced) from the input array, wherever, the difference is True (aka... 1) yielding what you see on line 6.
This is easily implemented in any tools that you have available. The only issue would be whether it is really important to retain the start position of the inputs... changing this might have some impact on the resultant and may have to be investigated.
You could also look at a first order or second order difference to decide on what type of differences you are interested. This can be done easily and is built-in to many languages (ie np.gradient in numpy)
Just some food for thought... might be better than just taking every 2nd, 3rd, 'x'rd point which is standard go-to