Planetary Coordinate Reference Systems
There is an interesting but perhaps little-used folder of *.prj files called “Solar System”. As someone interested in geodesy and its application it is particularly intriguing how scientists have constructed coordinate reference systems for planetary bodies other than the Earth.
First off let’s have a look at the details found in ArcGIS Desktop for "Geographic Coordinate Systems" of solar system objects. ArcGIS does not have any projected coordinate reference systems for the other planets and moons. Therefore you'll have to make a custom projection if you want to build upon the geographic coordinate system.
However, the folder contains coordinate reference systems for all the major objects found in the Solar System including all the planets, Jupiter's Moons and many others.

Let's start with the Moon
Apart from Earth, the Moon is arguably the astronomical body with the longest applied study of coordinate systems due to its long history of observation compared to other bodies. Interestingly, a standard Lunar Coordinate System was only agreed upon in 2006 for the Lunar Reconnaissance Orbiter mission and in 2008 a Lunar Geodesy and Cartography Working Group was created to maintain the current reference system.
Lunar coordinates, also known as Selenocentric coordinates, act in a similar way to those on Earth using the same nomenclature for geodetic longitude and latitude on Earth. As on Earth, latitude measures the distance north or south of an equator defined to be approximately 90° from the rotation axis, while longitude is measured east and west from an arbitrarily chosen central meridian.
On the Moon, the origin of the coordinate system passes through the point that is most nearly, on average, pointed towards the centre of the Earth. The "on average" part of the definition of the origin is because of precession, the change in the axis of rotation with respect to a reference plane.

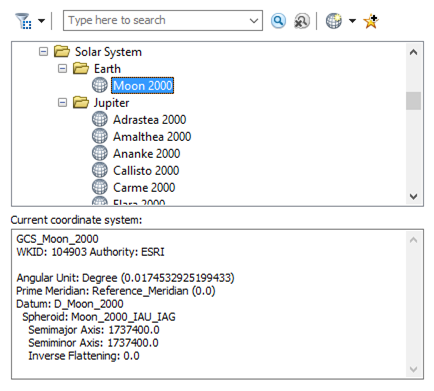
From the first image, it can be seen that the Moon is regarded as a perfect sphere (both semimajor and semiminor axis are the same value: 1737400.00 m).
Before we explore further there are two definitions that are important to know when working with planetary bodies:
Planetocentric coordinates (for the Moon selenocentric) - are expressed as coordinates with the origin at the center of mass of the body. The coordinates refer to the equatorial plane of the body concerned and are commonly used within calculations of celestial mechanics.
Planetographic coordinates (for the Moon selenographic) - are used for observations of the surface features of those planets whose figures are not truly spherical, but oblate. They are referred to the mean surface of the planet, and are the coordinates actually determined by observation.
The Moon uses selenocentric coordinates where Latitude is the angle between a line extending from the origin to the planetary equator and a vector to the point of interest. Longitude is the angle between this vector and the plane of the Prime Meridian measured in an eastern direction. Radius is the distance from the Moon’s center of mass to the point of interest. The radius of the Moon is defined as 1,737.4 km
Lunar Fixed Reference System
However, there are really two reference systems for the Moon and it has to do with the two definitions above. However, ArcGIS Desktop 10.3 only shows a selenocentric coordinate system. The principal difference between the following reference systems is how the Moon's axes are treated.
Mean Earth - Polar System a selenocentric system
The Mean Earth/Polar Axis reference system defines the z-axis as the mean rotational pole. The Prime Meridian (0˚ Longitude) is defined by the "mean Earth direction" (the point on the lunar surface designated as the origin, this happens to be close to the Oppolzer A crater, below). This system is used in operations for planning, observational targeting, geographic identification of lunar landforms, and inter-mission communications.

Principal Axis System a selenographic system
This system can be thought of as a body-fixed rotating coordinate system. The Moon principal axes are used but due to the Moon's rotating characteristics, tidally locked to the Earth, this system and the Mean Earth/Polar Axis System do not align. However, they can be aligned through a transformation method bringing the error down to approximately 1Km. The Principal Axis System is used for studies including gravity field survey and lunar laser ranging.
Key information and positioning of the Moon can be explored further using HORIZONS by JPL.
Selenocentric details as found in ArcGIS
GEOGCS["GCS_Moon_2000",DATUM["D_Moon_2000",SPHEROID["Moon_2000_IAU_IAG",1737400.0,0.0]],
PRIMEM["Reference_Meridian",0.0],UNIT["Degree",0.0174532925199433]]
Lunar Reconnaissance Orbiter
Explore the mapping created by the Lunar Reconnaissance Orbiter Camera on the LROC WMS Image Map.

And here's a great image I could not resist posting which was taken by the Lunar Reconnaissance Orbiter Camera of the Solar Eclipse on 21st August 2017.




 (Source:
(Source: