- Home
- :
- All Communities
- :
- Products
- :
- 3D
- :
- 3D Questions
- :
- Construct Points on polyline at 3d distance
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Construct Points on polyline at 3d distance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Greetings. I'm having trouble finding information on the construct points tool. I have about 100 separate hiking trails that have z geometry. I have calculated points at 1 mile intervals along the track using the Construct Points tool in the editor toolbar. The problem I'm having is determining whether these points are based on the surface distance or euclidean distance along the line. I can't seem to find any documentation on this in the help files or in the forum. Any insight? I can upload files if needed.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
In the absence of a statement, I would suspect that it would be 2D distance.
Creating new points along a line—Help | ArcGIS for Desktop
However, it is always best to test an unknown circumstance.
- On a horizontal line construct a point 1000 meters from an origin point
- assign z value 1000 meters greater than the origin point's Z and the angle
obviously, you should end up with a 45 degree angle and root 2 * 1000 m as the horizontal distance if the distance from the origin to destination was actually 3D. If you end up with X being 1000 meters greater, then it is 2D distance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Thanks for the reply and idea Dan. I created a 3d line with 45 degree angle as you mentioned. Turns out it does in fact use the 2d distance. One would think this would be a very trivial function, but apparently not.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I do understand the rationale however, if one is in the field gathering data with the worlds most precise instrument, you would have the option of determining position using a horizontal offset from a location or one that is "parallel" to a slope.
Considering the first case, you are measuring distance/offset between two points along a parallel plane (ie like using a level in the field for instance if you have ever done old-school surveying). You don't care about the intervening elevations and if you need Z, you simply determine the offset relative to the elevation to your origin point. You get an 'exact' measure of the distance and the coordinates, relative to the origin. If the distance is short enough you could confirm it with a tape measure.
In the second case, you measure along a slope... now think about it... you aren't actually measuring the distance along the slope since you are generalizing the surface by taking a line 'parallel' the surface between 2 points. How realistic is that assumption? Most people don't give a beaver dam, they just think... cool ... its more accurate. sorry, I can think of all kinds of surfaces where that assumption is just plain wrong.
Summary... (finally) I prefer that the distance between two points is 2D as is the determination of their coordinates. I then can make the overt statement/assumption that the elevation values between those two points can be used to "estimate" the slope length...aka distance between the 2 points... and I am confident that the locations are the same. Now you say, but I need a distance along the slope of 100 m and I am getting 120 m. So you cleverly do the math and come up with a new location...of course you now have to deal with the fact that you again have an "estimate" and the only thing that you can be sure of is the 2D location since the elevation at your new point may not be representative of the slope you estimated from your first guess.
Head hurt? good, stick with 2D distance and known coordinates, estimate 3D distance with your assumptions of the intervening terrain between them.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
It would be nice if there there were additional methods for 3D measurements. All methods are 2D on the polyline geometry. There is the segmentAlongLine method that mentions measures, so I was hopeful that converting the geometry to Polyline ZM would allow for extracting a sub-segment and use the lastPoint of the polyline to get the point. In a previous thread I published a snippet to convert a PolylineZ to PolylineZM and assign the 3D length as M value:
https://community.esri.com/message/516789#comment-516789
That turned out to be wrong. So I used the snippet and shaped it a little bit to create a positionAlongLine3D function.
def main(): import arcpy arcpy.env.overwriteOutput = True sr = arcpy.SpatialReference(28992) lst_coords = [[[0, 0, 0], [1000, 0, 0], [1000, 1000, 0], [0, 1000, 0], [0, 0, 0]], [[2000, 0, 0], [3000, 0, 1000], [3000, 1000, 2000], [2000, 1000, 3000], [2000, 0, 4000]]] lines = [] points = [] lines_m = [] points_m = [] points_ok = [] for feature in lst_coords: polyline = arcpy.Polyline( arcpy.Array([arcpy.Point(*coords) for coords in feature]), sr, True, False) lines.append(polyline) segment = polyline.segmentAlongLine(0, 2500, False) points.append(arcpy.PointGeometry(segment.lastPoint, sr, True, False)) polyline_zm = CreateZAwareFeature(polyline, sr) lines_m.append(polyline_zm) segment_m = polyline_zm.segmentAlongLine(0, 2500, False) points_m.append(arcpy.PointGeometry(segment_m.lastPoint, sr, True, True)) pnt_ok = positionAlongLine3D(polyline, 2500) points_ok.append(pnt_ok) arcpy.CopyFeatures_management(lines, r'C:\GeoNet\Query3DpointAndDistance\test.gdb\lines') arcpy.CopyFeatures_management(points, r'C:\GeoNet\Query3DpointAndDistance\test.gdb\points') arcpy.CopyFeatures_management(lines_m, r'C:\GeoNet\Query3DpointAndDistance\test.gdb\lines_m') arcpy.CopyFeatures_management(points_m, r'C:\GeoNet\Query3DpointAndDistance\test.gdb\points_m') arcpy.CopyFeatures_management(points_ok, r'C:\GeoNet\Query3DpointAndDistance\test.gdb\points_ok') def positionAlongLine3D(polyline_z, dist): length = 0 if dist <= 0: return arcpy.PointGeometry(polyline_z.firstPoint, polyline_z.spatialReference, True) elif dist >= polyline_z.length: return arcpy.PointGeometry(polyline_z.lastPoint, polyline_z.spatialReference, True) else: for part in polyline_z: cnt = 0 for pnt in part: if cnt == 0: pnt_prev = arcpy.Point(pnt.X, pnt.Y, pnt.Z) length += get3DLength(pnt, pnt_prev) if length > dist: d1 = dist - prev_length seg_length = length - prev_length frac = d1 / seg_length segment = arcpy.Polyline(arcpy.Array([pnt_prev, pnt]), polyline_z.spatialReference) pnt_3d = segment.positionAlongLine(frac, True) z = (1-frac) * pnt_prev.Z + frac * pnt.Z pntz = arcpy.Point(pnt_3d.firstPoint.X, pnt_3d.firstPoint.Y, z) return arcpy.PointGeometry(pntz, polyline_z.spatialReference, True) break cnt += 1 pnt_prev = pnt prev_length = length def CreateZAwareFeature(polyline_z, sr): lst_poly_zm = [] length = 0 for part in polyline_z: part_zm = [] cnt = 0 for pnt in part: if cnt == 0: pnt_prev = arcpy.Point(pnt.X, pnt.Y, pnt.Z) length += get3DLength(pnt, pnt_prev) pnt_zm = arcpy.Point(pnt.X, pnt.Y, pnt.Z, length) part_zm.append(pnt_zm) pnt_prev = arcpy.Point(pnt.X, pnt.Y, pnt.Z) cnt += 1 lst_poly_zm.append(part_zm) polyline_zm = arcpy.Polyline(arcpy.Array(lst_poly_zm), sr, True, True) return polyline_zm def get3DLength(pnt1, pnt2): return math.sqrt((pnt1.X - pnt2.X)**2 + (pnt1.Y - pnt2.Y)**2 + (pnt1.Z - pnt2.Z)**2) if __name__ == '__main__': main()
So the script creates two lines, the first is 2D (no Z) and the second has the same shape but the sides have an angle of 45° in Z direction, which mean that they are root(2) longer as shown in the field Length3D:
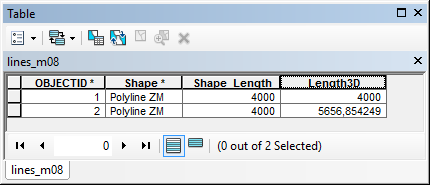
If you look at the lines in 2D they look the same, but the (3D) length isn't:

When you want to get the point at a distance of 2500m from the start in 3D the result should be:

... or looking at it in 3D:
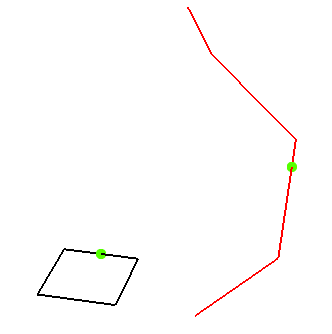
The alternative would be to use dynamic segmentation on the M-aware polylines.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Nice Xander... and given a coordinate from an origin you could then return the 2D and 3D distance in the table... with the implicit, but oft ignored assumption, that the slope along the line from start to destination is representative of the underlying terrain.
My beef is that some think a 3D distance/length is more accurate than 2D... it isn't, think of a cliff, even its slope and hence length with get averaged it you measure on either side of it.
On a similar vein, people have no problem understanding that Manhatten distance might be a better representation of distance on a rectilinear network, or network distance for that of less geometric configurations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I just added an idea on the idea site (since it is not yet possible on GeoNet) to request support for 3D and M value on ArcPy geometries:
ArcGIS Idea - Support for 3D methods and M values on ArcPy geometries
Please promote if you think this is a good idea.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Ive created an ArcMap add-in with the .NET sdk to construct points along a 3D polyline using the 3d distance. In arcobjects this is exposed through the ICurve3D interface. The add-in can be found on ArcGIS.com as Construct points along a 3D line.
An enhancement has been entered to update construct points for a future release. This also applies to Pro and the Pro SDK.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hey Sean - this addin is exactly what I need (I need to put a 5km marker for every 5km travelled on a trail). Is there a way to do this in Pro now - or is there a Pro Add In?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hey Dave,
Pro's 'construct points along a line' is still only 2D distance. A 3D distance option is on the todo list.
I'll probably end up porting the ArcMap add-in very soon though to cover the gap.