- Home
- :
- All Communities
- :
- Products
- :
- Spatial Statistics
- :
- Spatial Statistics Questions
- :
- Re: Emerging Hotspot Analysis - Help Understanding...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Emerging Hotspot Analysis - Help Understanding Outcomes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi,
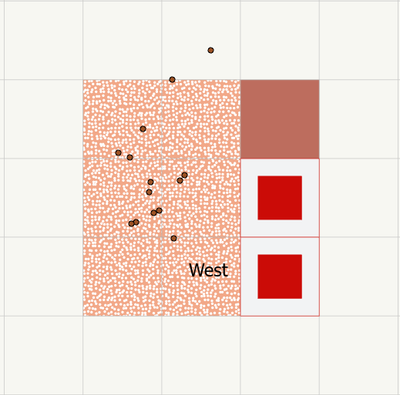
This maybe a silly question, but I have ran the emerging hotspot analysis, all works fine, but it's just a query with regarding to when I overlay my point data ontop of the suposedly "New Hot Spot" and others. Taking just one of these for example, I have a 1,375 fishnet grid square, with no dots in it at all, yet it's a "New Hot Spot". See image below:
My question: Is this right? If so, how do I articulate this, how can i increase the accuracy of this?7
Thanks in advance!
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
This is a great question! Thanks for asking it.
Sometimes I think these tools should be called hot regions, rather than hot spots. Conceptually, they work by visiting each bin in the cube and computing the mean value for that bin and all it's space-time neighbors. It then compares that local mean to the global mean (the mean for all bins in the cube since you used Entire Cube for the Global Window parameter). So even if there aren't any points in a New Hot Spot bin, if the local mean for that bin and it's space-time neighbors is hot, you can still have a new hot spot.
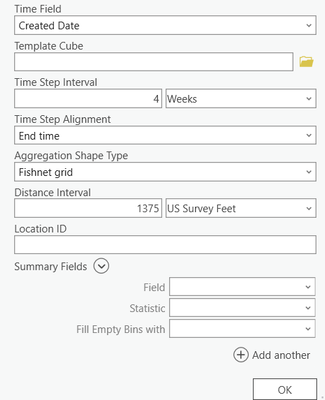
Let me try to put it into the context of your analysis. It looks like you used Create Space Time Cube by Aggregating Points. You said you wanted each fishnet bin to be about 1/4 square mile by 4 weeks. Great. Then you ran Emerging Hot Spot Analysis and defined the spatial-temporal neighborhood to extend 1/2 mile around each bin and one time step previous (so the current time step plus the previous time step... encompassing 8 weeks).
Several bins in your graphic are sporadic hot spots, so sometimes the mean for those bins and their space time neighbors were hot spots and sometimes they weren't, but they WERE hot for the last (most recent) time step. One of the bins is a consecutive hot spot, so for the last time step and at least one other immediately previous time step (fewer than 90%, though), it was a statistically significant hot spot (the local mean was significantly higher than the global mean). For the new hot spot bins, only the last (most recent) time step is hot. Even though there aren't any points in those bins (according to the graphic), the local neighborhoods have points that apparently make those bins hot. Maybe look at the 3D version of the cube columns. I don't know what the points represent, but the pattern might suggest a spreading process to the east ??
Also, I'm not sure if your image is showing ALL points in one part of your study area or just points for the last 4 weeks. If it is ALL points, you will clearly have a LOT of zero bins in your cube. In that case, the global mean is zero and it doesn't take many points in a neighborhood to create a hot spot (since finding a point is soooo very rare). My own feeling is that a ton of zeros (the vast majority) makes the analysis unstable. Perhaps you can increase bin size so you have fewer zero bins? I'm not sure what your points represent but I might have other ideas if indeed you are dealing with a cube that is almost entirely zeros.
I hope this helps! Thanks again for your question, Stephen!
Lauren Griffin, Esri
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
This is a great question! Thanks for asking it.
Sometimes I think these tools should be called hot regions, rather than hot spots. Conceptually, they work by visiting each bin in the cube and computing the mean value for that bin and all it's space-time neighbors. It then compares that local mean to the global mean (the mean for all bins in the cube since you used Entire Cube for the Global Window parameter). So even if there aren't any points in a New Hot Spot bin, if the local mean for that bin and it's space-time neighbors is hot, you can still have a new hot spot.
Let me try to put it into the context of your analysis. It looks like you used Create Space Time Cube by Aggregating Points. You said you wanted each fishnet bin to be about 1/4 square mile by 4 weeks. Great. Then you ran Emerging Hot Spot Analysis and defined the spatial-temporal neighborhood to extend 1/2 mile around each bin and one time step previous (so the current time step plus the previous time step... encompassing 8 weeks).
Several bins in your graphic are sporadic hot spots, so sometimes the mean for those bins and their space time neighbors were hot spots and sometimes they weren't, but they WERE hot for the last (most recent) time step. One of the bins is a consecutive hot spot, so for the last time step and at least one other immediately previous time step (fewer than 90%, though), it was a statistically significant hot spot (the local mean was significantly higher than the global mean). For the new hot spot bins, only the last (most recent) time step is hot. Even though there aren't any points in those bins (according to the graphic), the local neighborhoods have points that apparently make those bins hot. Maybe look at the 3D version of the cube columns. I don't know what the points represent, but the pattern might suggest a spreading process to the east ??
Also, I'm not sure if your image is showing ALL points in one part of your study area or just points for the last 4 weeks. If it is ALL points, you will clearly have a LOT of zero bins in your cube. In that case, the global mean is zero and it doesn't take many points in a neighborhood to create a hot spot (since finding a point is soooo very rare). My own feeling is that a ton of zeros (the vast majority) makes the analysis unstable. Perhaps you can increase bin size so you have fewer zero bins? I'm not sure what your points represent but I might have other ideas if indeed you are dealing with a cube that is almost entirely zeros.
I hope this helps! Thanks again for your question, Stephen!
Lauren Griffin, Esri
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi Lauren,
Thanks so much for your detailed response! I am keen in discussing your thoughts / other options to deal with lots of bins that are empty whilst still being able to keep the bin/cell size relatively small so that we can pinpoint changes.
Regards,
Steve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
If we figure out anything that may be helpful to others, I’ll ask you to please post what we learn to the community 😊
Lauren
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
No problem at all!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hello--
I've come across an issue similar to the one you had, Stephen. I am running the Emerging Hotspot Analysis on 2,101 points (from Jan 1, 2019 through April 30, 2023) in a single county. The first screenshot shows the spread of my points across a grid covering the entire county.
As you can see, most of the hexagons do not even have any points, but we needed to create an entire county-level grid (each hex width=0.68 miles) for this ongoing project to account for the possibility that future incidents could occur in any single hexagon as we re-run the analysis with new data on a monthly basis.
When I created the space time cube and chose the option to fill empty bins with zero, I found that 42,669 of the 44,100 time-step bins have zeros.
I know that is a lot of zeros, but ran Emerging Hotspot Analysis with the following parameters to see what would happen:
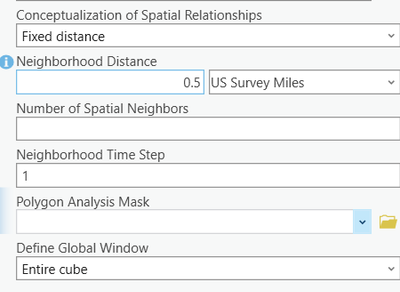
- 'Fixed Distance' with a 'Neighborhood Distance' of 2.24 miles.
- (hex size and neighborhood distance are small, but we would like the most granular scale possible for this particular analysis).
- 6 Spatial Neighbors
- 1 Neighborhood Timestep
- "Define Global Window" with 'Individual Timestep".
- (I chose this option because our primary area of concern is to identify the most recent trends as we monitor the data on a monthly basis).
When I ran the analysis, my results shown a "New Hotspot" where no incidents have occurred. (See second screenshot) There are 2 incidents within 6 spatial neighboring hexagons that occurred within 2 weeks of each other, but that doesn't seem enough to qualify as a new hotspot.
Any advice on how to potentially mitigate the effect of bins with lots of zeros? Can you include the entire grid for the analysis in order to account for the possibly of future incident occurrence in a hexagon, but somehow drop the zeros to un-skew the global mean?.
Thank you!! ~Ashley