How to find the maximum rectangle contained within a polygon

Anonymous User · ‎08-25-2016

Hi.

There is are arcmap tools that can return a bounding box/rectangle/envelope etc for a given feature (e.g. set of points, line or polygon). I am trying to find a similar tool that will return the maximum rectangle that can be created that is *contained within* the features.

Here is a link to the Arcmap/Pro tool:

Minimum Bounding Geometry—Data Management toolbox | ArcGIS for Desktop

Here is a link to someone else's StackExchange question that explains fairly well with diagrams what I am trying to achieve:

geometry - How to find the maximum-area-rectangle inside a convex polygon? - Geographic Information ...

Would be interested to know if anyone has already solved this using existing Arcmap tools without delving into complicated scripts...?

Cheers

-Paul

DanPatterson_Retired · ‎08-25-2016

looked but very limited 'market' and only esoterically interesting (unless you are trying to squeeze a building footprint on too small a lot).

Having lookin into the problem Bill Huber alludes to in your link..., and I think correctly so, that this problem is a bit more difficult than one would think.

@csd That's a great point, but Saryk is still correct, as my counterexample shows. Saryk, there is no problem with the minimum area bounding rectangle: it's easy to prove (rigorously) that it must include a side of the convex hull. I believe the maximum area inscribed rectangle (of a convex polygon) need only have two vertices touching the boundary, no more. – whuber♦ Oct 3 '13 at 15:03

Since you appear to be working with points, you could minimize your candidates by constructing a triangulation, and keep the largest triangles. If they were adjacent, that would be useful, but at least you could remove the fluff from the input points.

Anonymous User · ‎08-25-2016

Thanks for the reply Dan. Good at least to know there's nothing 'out of the box' in ArcMap before moving forward - I'd hate to reinvent the wheel!

Your building footprint comment is right on the money - use case involves polygons which are parcels of land where we need to find the maximum rectangular shape that we can place onto it.

If anyone else has any comments or suggestions they would be appreciated, else I'll press on with attempting to put something together...

Cheers.

DanPatterson_Retired · ‎08-25-2016

Now if you only had a few to do, I would begin with forming a rectangle along the longest side of the polygon and extending the rectangle upward/normal to that and pick the shorted intersection point with the otherside of the polygon. That would give you a right-angle triangle, hence, the rectangle. You could then sequentially shorten that line from one end or the other and repeat, checking the intersection triangle and area. Obviously a perfect rectangle would be easy, but picture this being applied to a trapezoid shaped lot... there would be some possibilities

PS... the triangulation would help with the visualization, since you could form right angle triangles from isoceles triangles should they arise in the process

XanderBakker · ‎08-27-2016

I had a go at this last night, with this polygon:

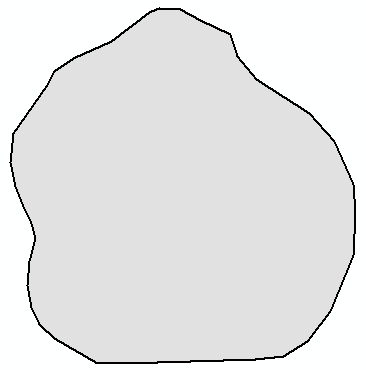
The code I used added all the rectangles created in the process (drawn using a color based on the area):

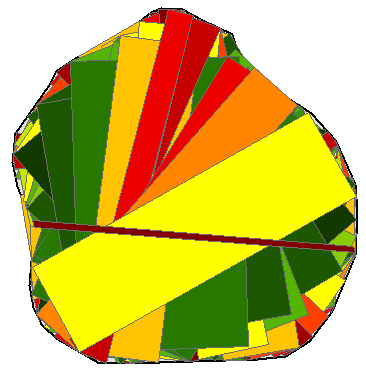
The largest polygon was this on:

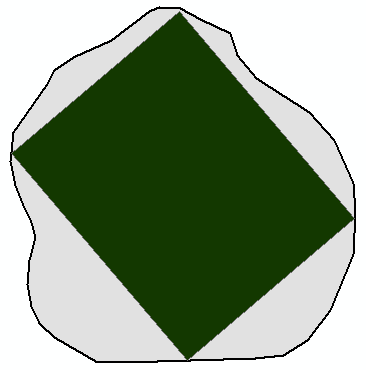
Which doesn't look that bad, although there are many things that will go wrong with the code. The idea I used was to get a first point on the boundary of the polygon, and select a second point on the boundary and have the points move around to get many combinations. These two points are treated as a side of the rectangle to be generated (one should also consider that the points could be used as diagonal of the rectangle). For this side, the perpendicular lines at start and end are created and intersected with the polygon (you should consider multipart results). The shortest line length is applied to the other line and the rectangle is created.

This is the code I came up with:

#-------------------------------------------------------------------------------
# Name:        max_inscribing_rectangle.py
# Purpose:     get maximum inscribing rectangle for polygon
#
# Author:      Xander
#
# Created:     26-08-2016
#-------------------------------------------------------------------------------

def main():
    import arcpy
    arcpy.env.overwriteOutput = True

    fc = r'C:\GeoNet\MaximumAreaInscribedRectangle\data.gdb\polygon'
    fc_out = r'C:\GeoNet\MaximumAreaInscribedRectangle\data.gdb\rectangles01'

    # get polygon
    polygon = arcpy.da.SearchCursor(fc, ('SHAPE@')).next()[0]
    sr = polygon.spatialReference

    # determine outline, extent and diagonal
    polyline = polygon.boundary()
    extent = polygon.extent
    diagonal_length = getPythagoras(extent.width, extent.height)

    lst_rectangles = []
    # first loop for start point of first side
    for i in range(10):
        perc_p1 = float(i) / 10
        pntg1 = polyline.positionAlongLine(perc_p1, True)

        # second loop end point of first side
        for j in range(10):
            frac = float(j) / 20
            perc_p2 = perc_p1 + 0.25 + frac
            if perc_p2 > 1:
                perc_p2 -= 1
            pntg2 = polyline.positionAlongLine(perc_p2, True)

            # process as side
            # - get angle between points
            angle = getAngle(pntg1, pntg2)

            # - create perpendicual lines at start and end
            pntg1a = pntg1.pointFromAngleAndDistance(angle + 90, diagonal_length, 'PLANAR')
            pntg1b = pntg1.pointFromAngleAndDistance(angle - 90, diagonal_length, 'PLANAR')
            line1 = createStraightLine(pntg1a, pntg1b)

            pntg2a = pntg2.pointFromAngleAndDistance(angle + 90, diagonal_length, 'PLANAR')
            pntg2b = pntg2.pointFromAngleAndDistance(angle - 90, diagonal_length, 'PLANAR')
            line2 = createStraightLine(pntg2a, pntg2b)

            # - intersect by polygon (asume single parts)
            line1cut = checkInvertedLine(line1.intersect(polygon, 2), pntg1)
            line2cut = checkInvertedLine(line2.intersect(polygon, 2), pntg2)

            # - determine shortest, cut other by length shortest
            length1 = line1cut.length
            length2 = line2cut.length
            if length2 < length1:
                # cut line 1
                line1cut = line1cut.segmentAlongLine(0, length2, False)
            else:
                # cut line 2
                line2cut = line2cut.segmentAlongLine(0, length1, False)

            # - form rectangle and add to list
            rectangle = createRectanglePolygon(line1cut, line2cut)
            lst_rectangles.append(rectangle)

            # process point pair as diagonal of rectangle?

    # write output
    arcpy.CopyFeatures_management(lst_rectangles, fc_out)


def createRectanglePolygon(line1, line2):
    sr = line1.spatialReference
    pnt1a = line1.firstPoint
    pnt1b = line1.lastPoint
    pnt2a = line2.firstPoint
    pnt2b = line2.lastPoint
    return arcpy.Polygon(arcpy.Array([pnt1a, pnt1b,
                                      pnt2b, pnt2a,
                                      pnt1a]), sr)


def checkInvertedLine(line, pntg):
    # start of line should be near pntg
    sr = line.spatialReference
    pnt_start = line.firstPoint
    pnt_end = line.lastPoint
    dist_start = getPythagoras(pnt_start.X-pntg.firstPoint.X,
                               pnt_start.Y-pntg.firstPoint.Y)
    dist_end = getPythagoras(pnt_end.X-pntg.firstPoint.X,
                               pnt_end.Y-pntg.firstPoint.Y)
    if dist_end < dist_start:
        # flip
        return arcpy.Polyline(arcpy.Array([pnt_end, pnt_start]), sr)
    else:
        return line

def createStraightLine(pntg1, pntg2):
    sr = pntg1.spatialReference
    return arcpy.Polyline(arcpy.Array([pntg1.firstPoint, pntg2.firstPoint]), sr)

def getAngle(pntg1, pntg2):
    '''Define angle between two points'''
    return pntg1.angleAndDistanceTo(pntg2, 'PLANAR')[0]

def getPythagoras(w, h):
    import math
    return math.hypot(w, h)


if __name__ == '__main__':
    main()
‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

It is not much, but maybe a start...

DanPatterson_Retired · ‎08-27-2016

Looks good. perhaps Paul could pop off a few real world lots (pie shaped would be worst case scenario)

If he could also provide municipal lot offsets (side, rear, front), your shapes and vertices will be greatly simplified.

Oliver_Burdekin · ‎06-05-2018

Thanks Xander, I was looking for something like this. The code seems to trip up when trying it with more complex and non-convex polygons but simplyfying my input got the desried result. You might also be interested in this d3plus implementation of the largest rectangle problem:

https://d3plus.org/blog/behind-the-scenes/2014/07/08/largest-rect/

Cheers,

Oliver

XanderBakker · ‎06-05-2018

Nice!

DanPatterson_Retired · ‎06-05-2018

Cool! another algorithm to play with!

wlew · ‎11-27-2020

Hi Xander,

I am looking at your example above and came up with my own polygon shape file. However, I ran into this one issue when I was running the code and I'm not sure why there is this error with _base.py in arcPy where

...line 98, in checkInvertedLine
pnt_start = line.firstPoint
File "C:\Program Files\ArcGIS\Pro\Resources\ArcPy\arcpy\arcobjects\_base.py", line 90, in _get
return convertArcObjectToPythonObject(getattr(self._arc_object, attr_name))
SystemError: <built-in function getattr> returned NULL without setting an error

Have you encountered this error before?