Python 2.7 Determine inner ring in JSON

[JamesCrandall]

Trying to calculate acreage/area from polygon array loaded from JSON result of map service query and running into issue with geometries that contain "holes".  From what I know, the first list of coordinate pairs (index 0) is the "outer" polygon, then all other coordinate pairs would be the interior rings.  This is easiest enough to setup a condition to identify and calculate total area.  For example area of a polygon with two interior rings could be determined by:

ring[0] area - ring[1] area - ring[2] area = total area

Got it.  However, what if the polygon consists of 1 ring with interior rings and a ring coincident.  That is, there are what looks like 2 polygons coincident to each other but one of them contains holes. 

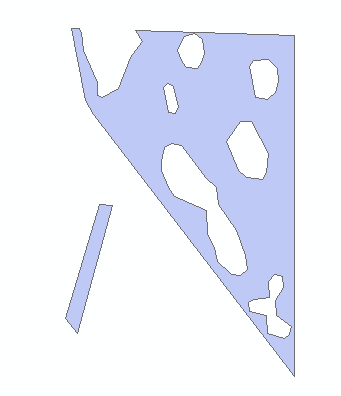
How do I come up with the total area in this case?  Example below shows 2 coincident polygons, 1 with holes that needs to have the area of interior rings subtracted from the overall ring, while the coincident polygon only has 1 ring that must be added to the total area.

Edit: to simplify my question, how do I arrive at the count of 2 rings (area of 1 "island" ring, area 1 outer ring - total area of 7 interior rings)

 Here's the json for the rings in picture:

{
        "rings" : [
          [
            [
              -8960520,
              3141929
            ],
            [
              -8960482,
              3141916
            ],
            [
              -8960381,
              3141979
            ],
            [
              -8960297,
              3142183
            ],
            [
              -8960220,
              3142291
            ],
            [
              -8960267,
              3142363
            ],
            [
              -8959212,
              3142329
            ],
            [
              -8959216,
              3140075
            ],
            [
              -8960546,
              3141806
            ],
            [
              -8960599,
              3141897
            ],
            [
              -8960692,
              3142376
            ],
            [
              -8960637,
              3142374
            ],
            [
              -8960622,
              3142346
            ],
            [
              -8960608,
              3142230
            ],
            [
              -8960516,
              3142015
            ],
            [
              -8960520,
              3141929
            ]
          ],
          [
            [
              -8960049,
              3141823
            ],
            [
              -8960001,
              3141812
            ],
            [
              -8959983,
              3141860
            ],
            [
              -8960017,
              3141990
            ],
            [
              -8960058,
              3142011
            ],
            [
              -8960083,
              3141987
            ],
            [
              -8960049,
              3141823
            ]
          ],
          [
            [
              -8959472,
              3141918
            ],
            [
              -8959391,
              3141908
            ],
            [
              -8959340,
              3141951
            ],
            [
              -8959320,
              3142025
            ],
            [
              -8959325,
              3142112
            ],
            [
              -8959387,
              3142168
            ],
            [
              -8959484,
              3142163
            ],
            [
              -8959513,
              3142124
            ],
            [
              -8959472,
              3141918
            ]
          ],
          [
            [
              -8959828,
              3142151
            ],
            [
              -8959808,
              3142211
            ],
            [
              -8959826,
              3142302
            ],
            [
              -8959875,
              3142344
            ],
            [
              -8959943,
              3142320
            ],
            [
              -8959986,
              3142228
            ],
            [
              -8959959,
              3142148
            ],
            [
              -8959927,
              3142120
            ],
            [
              -8959858,
              3142113
            ],
            [
              -8959828,
              3142151
            ]
          ],
          [
            [
              -8959663,
              3141625
            ],
            [
              -8959585,
              3141438
            ],
            [
              -8959535,
              3141389
            ],
            [
              -8959428,
              3141379
            ],
            [
              -8959399,
              3141424
            ],
            [
              -8959384,
              3141551
            ],
            [
              -8959497,
              3141761
            ],
            [
              -8959571,
              3141760
            ],
            [
              -8959663,
              3141625
            ]
          ],
          [
            [
              -8959960,
              3141599
            ],
            [
              -8960028,
              3141615
            ],
            [
              -8960074,
              3141591
            ],
            [
              -8960098,
              3141499
            ],
            [
              -8960095,
              3141436
            ],
            [
              -8960049,
              3141324
            ],
            [
              -8960008,
              3141263
            ],
            [
              -8959800,
              3141169
            ],
            [
              -8959793,
              3141018
            ],
            [
              -8959741,
              3140928
            ],
            [
              -8959722,
              3140834
            ],
            [
              -8959630,
              3140750
            ],
            [
              -8959570,
              3140741
            ],
            [
              -8959528,
              3140782
            ],
            [
              -8959542,
              3140877
            ],
            [
              -8959601,
              3141041
            ],
            [
              -8959719,
              3141213
            ],
            [
              -8959733,
              3141325
            ],
            [
              -8959797,
              3141385
            ],
            [
              -8959960,
              3141599
            ]
          ],
          [
            [
              -8959346,
              3140751
            ],
            [
              -8959388,
              3140703
            ],
            [
              -8959379,
              3140596
            ],
            [
              -8959479,
              3140586
            ],
            [
              -8959518,
              3140560
            ],
            [
              -8959514,
              3140503
            ],
            [
              -8959403,
              3140475
            ],
            [
              -8959393,
              3140355
            ],
            [
              -8959278,
              3140327
            ],
            [
              -8959249,
              3140351
            ],
            [
              -8959237,
              3140406
            ],
            [
              -8959333,
              3140479
            ],
            [
              -8959343,
              3140579
            ],
            [
              -8959291,
              3140665
            ],
            [
              -8959296,
              3140732
            ],
            [
              -8959346,
              3140751
            ]
          ],
          [
            [
              -8960421.4573999997,
              3141207.5951999985
            ],
            [
              -8960651.4805999994,
              3140355.0742999986
            ],
            [
              -8960730.3613000009,
              3140457.7377999984
            ],
            [
              -8960501.8148999996,
              3141210.1849000007
            ],
            [
              -8960421.4573999997,
              3141207.5951999985
            ]
          ]
        ]
      }

[jcarlson]

Polygons ought to follow the right-hand rule, i.e., outer rings go counter-clockwise, inner rings (holes) go clockwise. So if you first check the direction of the polygon vertices, you can then calculate (sum of right-hand areas) - (sum of left-hand areas).

[JamesCrandall]

Is direction guaranteed and how is direction determined?  Does it matter how the polygon was digitized (ie. an island polygon that was digitized clockwise)?

Thanks Josh!

Thanks!

[jcarlson]

You know, I'm not really sure. I've worked with querying a REST URL and using the returned JSON, only to have the resulting polygons be flagged as "invalid", and I ended up getting really strange area calculations.

As far as "how do you tell", you can check out this great Stack Overflow answer.

Is there a reason you have to work with the polygons this way, by the way?

[JamesCrandall]

These are geometries created by web tools, unvalidated / uncontrolled (the users can create any kind of whacked-out polygon imaginable) so I think I may have to just pursue getting out of reading ring coordinate all together and just convert the JSON to a feature class.  Then reading geometries via da.cursor is probably going to be much easier/cleaner way.

[DanPatterson]

clockwise outer rings and cc-wise inner rings give rise to negative areas using the "shoelace" formula (most gis packages implement this in some form or another). 

Reverse that and the areas are positive.  If somehow inner and outer are both going in the same direction or aren't enclosed in the outer ring, then all bets are off.