Feet to Decimal Degrees function

ChrisMathers · ‎10-31-2012

If there is a quicker way to do this conversion let me know (but I will still finish this for the fun of it regardless :D). I was looking for a way to take the state plane coords in feet from a polygon centroid and convert to decimal degrees. I found this post from 2002 http://forums.esri.com/Thread.asp?c=64&f=792&t=67737 which has a funtion to do just that. Its in VB but the trouble isn't converting that over to Python, its that I cant find all of the constants I need.

The script is for Washington State South NAD27 and I use Florida State North NAD83. The constants are all in the projection file for Florida North NAD83 except the major radius and the eccentricity. I looked in the projection file for NAD83 and saw that it is built on the GRS1980 spheroid. The Wikipedia page for that spheroid doesn't have those values and there isn't and page dedicated to the values for NAD83. At lease the GRS1980 values which seem to be the ones I may need are named differently from the script so I cant tell if they are the right ones. Any help? I will post this once I get it converted for anyone to steal for their own projects.

JakeSkinner · ‎10-31-2012

Hi Chris,

You can achieve this using an Update Cursor. Cursors give you have the ability to set a working coordinate system. Take a look at the 5th post here.

ChrisMathers · ‎10-31-2012

Well that is easier. Going to finish anyways. its important to know how these things work!

ChrisSnyder · ‎10-31-2012

BTW: in v10.1 there are no more .prj files, and you need to track down the projection codes (the prj code for WGS84 is 4326). So that would be the Spatial reference code you could use in the cursor provided you wanted to return WGS84 coordinates. You can also use the SR name, but good luck tracking down which SR "name" is the correct one (is it "WGS 84" or "GCS_WGS_1984").

Also, unless I am mistaken, the cursor SR parameter doesn't allow for datum transformations, so things could be off by quite a bit.

Safe method:
1. Project your centroid points (using the appropriate datum transformation)
2. Read the coordinates in a search cursor

NobbirAhmed · ‎10-31-2012

Assuming the coordinates in feet are stroed in a point feature class, you can use Convert Coordinate Notation tool (Data Management > Projections and Transformations) to get coordinate values in decimal degrees.

ChrisMathers · ‎11-01-2012

OK so not much was really needed to take that code and make it work. And it really does work. Ive taken the coordinates in feet and run them through then compared them to the decimal degrees I can get with 'calculate geometry' and they are the same. I will play with all these methods and see which one I like incorporating the best.

def Ft_DD(x,y):
    ## This function converts coordinates from Florida State Plane North Zone NAD83 feet
    ## to Geographic coordinates in decimal degrees
    ##
    ## The formula this program is based on are from "Map Projections,
    ## A Working Manual" by John P. Snyder, U.S. Geological Survey
    ## Professional Paper 1395, 1987, pages 295-298
    ##
    ##Function originally provided by Dan Saul, Washington State Department of Ecology
    ##
    ## Set up the coordinate system parameters.
    A = 20925604.47                         ## major radius of GRS 1980 ellipsoid, feet
    Ec = 0.0818191910435                    ## eccentricity of GRD 1980 ellipsoid
    Ec2 = Ec * Ec                           ## eccentricity squared
    AngRad = 0.017453292519943299           ## number of radians in a degree
    Pi4 = 3.141592653582 / 4                ## Pi / 4
    P1 = 29.583333333333329000 * AngRad     ## latitude of first standard parallel
    P2 = 30.750000000000000000 * AngRad     ## latitude of second standard parallel
    P0 = 29.000000000000000000 * AngRad     ## latitude of origin
    M0 = -84.5 * AngRad                     ## central meridian
    X0 = 1968500.0                          ## False easting of central meridian, map units

    ## Calculate the coordinate system constants.
    m1 = math.cos(P1) / math.sqrt(1 - (Ec2 * pow((math.sin(P1)),2)))
    m2 = math.cos(P2) / math.sqrt(1 - (Ec2 * pow((math.sin(P2)),2)))
    t1 = math.tan(Pi4 - (P1 / 2)) / pow((1 - Ec * math.sin(P1)) / (1 + Ec * math.sin(P1)),(Ec/2))
    t2 = math.tan(Pi4 - (P2 / 2)) / pow((1 - Ec * math.sin(P2)) / (1 + Ec * math.sin(P2)),(Ec/2))
    t0 = math.tan(Pi4 - (P0 / 2)) / pow((1 - Ec * math.sin(P0)) / (1 + Ec * math.sin(P0)),(Ec/2))
    n = math.log(m1 / m2) / math.log(t1 / t2)
    F = m1 / (n * pow(t1,n))
    rho0 = A * F * pow(t0,n)
    ## Convert the coordinate to Latitude/Longitude.

    ## Calculate the Longitude.
    x = x - X0
    Pi2 = Pi4 * 2
    rho = math.sqrt(pow(x,2) + (pow(rho0 - y,2)))
    theta = math.atan(x/(rho0 - y))
    t = pow(rho / (A * F),(1 / n))
    LonR = theta / n + M0
    x = x + X0

    ## Estimate the Latitude
    Lat0 = Pi2 - (2 * math.atan(t))

    ## Substitute the estimate into the iterative calculation that
    ## converges on the correct Latitude value.
    part1 = (1 - (Ec * math.sin(Lat0))) / (1 + (Ec * math.sin(Lat0)))
    LatR = Pi2 - (2 * math.atan(t * pow(part1,(Ec/2))))
    
    Lat0 = LatR
    part1 = (1 - (Ec * math.sin(Lat0))) / (1 + (Ec * math.sin(Lat0)))
    ##LatR = Pi2 - (2 * math.atan2((t * (part1**(Ec/2))),1))
    LatR = Pi2 - (2 * math.atan(t * pow(part1,(Ec/2))))
    print LatR,LonR
   
    if (abs(LatR - Lat0) > 0.000000002):
        ## Convert from radians to degrees.
        Lat = LatR / AngRad
        Lon = LonR / AngRad
    print str(Lon) + "|" + str(Lat)

LubicaCverckova2 · ‎04-02-2018

Hi Chris,

I need to do similar conversion of California II State Plane in US Survey feet to geographic coordinates in decimal degrees. I am not totally comfortable with python but need to have it in python. I updated the parameters in California values. But not getting desired output. Here is the updated part of the script your wrote in California values:

A = 20925604.47 ## major radius of GRS 1980 ellipsoid, feet
Ec = 0.0818191910435 ## eccentricity of GRD 1980 ellipsoid
Ec2 = Ec * Ec ## eccentricity squared
AngRad = 0.017453292519943299 ## number of radians in a degree
Pi4 = 3.141592653582 / 4 ## Pi / 4
P1 = 38.33333333 * AngRad ## latitude of first standard parallel
P2 = 39.83333333 * AngRad ## latitude of second standard parallel
P0 = 37.66666667 * AngRad ## latitude of origin
M0 = -122 * AngRad ## central meridian
X0 = 6561666.66666667 ## False easting of central meridian, map units

And here is the snapshot of Data Source:

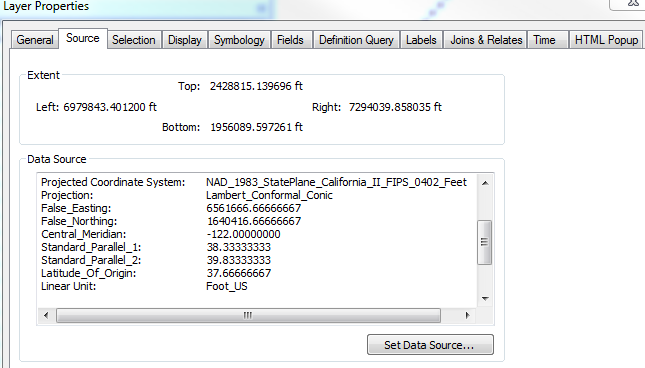
Unsure where the problem is. If it is due to no parameter for False northing or...?

Basically, the sample CA State Plane II x,y: 7079975.52661,2184310.50409 should give me: 39.1457869, -120.1722625 and if I run your code with above updated parameters, I am getting: 43.642324406, -120.048031426.

Any ideas how to fix that would be great!!!

RandyBurton · ‎04-02-2018

An alternative perhaps:

import arcpy  

x = 7079975.52661  
y = 2184310.50409  

# WGS 1984 : (4326) Lat/Lon  
# NAD_1983_2011_StatePlane_California_II_FIPS_0402_Ft_US - WKID: 6418 

ptGeometry = arcpy.PointGeometry(arcpy.Point(x,y),arcpy.SpatialReference(6418)).projectAs(arcpy.SpatialReference(4326))  

# print ptGeometry.JSON  
print ptGeometry.firstPoint.X, ptGeometry.firstPoint.Y  

# Result:  -120.172262515 39.1457869508‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

LubicaCverckova2 · ‎04-03-2018

Thank you Randy. It worked!