Create a multipart polygon with arcpy

[XanderBakker]

I am trying to create a multipart polygon based on 3 x 5 squares, but when I look at the result it dissolves the polygons and the enclosed squares are no longer part of it. If I do the same and store the result as a line (also multipart), the inner parts do appear in the result.

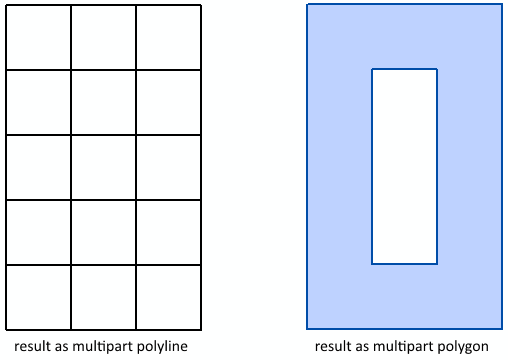
Can anyone explain me what I am doing wrong or show me how I can create a valid multipart polygon that consists in this case of 15 partes?

This is the code that I used.

import arcpy

# a square
part = [[0,0],[0,1],[1,1],[1,0],[0,0]]

mp = []
for x_shift in range(0,3):
    for y_shift in range(0,5):
        part_new = [[x+x_shift,y+y_shift] for [x,y] in part]
        print part_new
        mp.append(part_new)

# the nested list for the multipart
##mp = [[[0, 0], [0, 1], [1, 1], [1, 0], [0, 0]],
##      [[0, 1], [0, 2], [1, 2], [1, 1], [0, 1]],
##      [[0, 2], [0, 3], [1, 3], [1, 2], [0, 2]],
##      [[0, 3], [0, 4], [1, 4], [1, 3], [0, 3]],
##      [[0, 4], [0, 5], [1, 5], [1, 4], [0, 4]],
##      [[1, 0], [1, 1], [2, 1], [2, 0], [1, 0]],
##      [[1, 1], [1, 2], [2, 2], [2, 1], [1, 1]],
##      [[1, 2], [1, 3], [2, 3], [2, 2], [1, 2]],
##      [[1, 3], [1, 4], [2, 4], [2, 3], [1, 3]],
##      [[1, 4], [1, 5], [2, 5], [2, 4], [1, 4]],
##      [[2, 0], [2, 1], [3, 1], [3, 0], [2, 0]],
##      [[2, 1], [2, 2], [3, 2], [3, 1], [2, 1]],
##      [[2, 2], [2, 3], [3, 3], [3, 2], [2, 2]],
##      [[2, 3], [2, 4], [3, 4], [3, 3], [2, 3]],
##      [[2, 4], [2, 5], [3, 5], [3, 4], [2, 4]]]

# construct the array for the feature
lst_part = []
for part in mp:
    lst_pnt = []
    for pnt in part:
        lst_pnt.append(arcpy.Point(float(pnt[0]), float(pnt[1])))
    lst_part.append(arcpy.Array(lst_pnt))
array = arcpy.Array(lst_part)

# handle the array as polygon
polygon = arcpy.Polygon(array)
arcpy.CopyFeatures_management([polygon], r"D:\Xander\GeoNet\MultiPart\data.gdb\test_pol_mp")
print "Polygon partCount : {0}".format(polygon.partCount)
print "Polygon pointCount: {0}".format(polygon.pointCount)

# handle the array as polyline
polyline = arcpy.Polyline(array)
arcpy.CopyFeatures_management([polyline], r"D:\Xander\GeoNet\MultiPart\data.gdb\test_line_mp")
print "Polyline partCount : {0}".format(polyline.partCount)
print "Polyline pointCount: {0}".format(polyline.pointCount)

[DanPatterson_Retired]

Xander,

Messy code attached, but you catch the drift.  This is one of several methods that I have been experimenting with, but have a look.  In this one, I took the "ring" approach.  I can send you more details and a project offline if you want as well.  This is written very detailed so I can see what was needed to produce donuts, multiparts and the likes.  It use rectangles.  Another variant is in one of my two blog posts for both rectangular and hexagonal sampling frameworks, rotated or not.  Enjoy

'''
create_polygon_demo.py
Author:   Dan.Patterson@carleton.ca
Date:     Jan-Feb, 2015
Modified: lots
Purpose:
  To demonstrate the various types of polygons
  that can be formed from rings.  This is presented as detailed as
  possible so that the formation of any type of polygon can be seen
  from the points forming the rings.
Requires:
  A spatial reference...never make geometry without one.
Comments:
  It is setup so that you can comment or uncomment various sections
  and change the file name.  Since, CopyFeatures_Management is used
  it will NOT overwrite existing files, so, remove them from ArcMap,
  delete any file you want to overwrite and run again, or use a
  different file name.
  The files have already been created and are contained in the folder
  with the project.
  
'''
def union_poly(polygons):
  '''union a list of polygons, results can be unexpected'''
  newPoly = polygons[0]
  for i in range(1,len(polygons)):
    polyunion = newPoly.union(polygons)
    newPoly=polyunion
  return newPoly
def polygonize(ring_list,output_shp,SR=3395,union=False,replace=True):
  '''create polygons,from rings (list of points) with a specify SR.
     default SR 'WGS_1984_World_Mercator' if unspecified. rings can
     include exterior and interior point lists'''
  polygons = []
  for i in ring_list:
    arr = arcpy.Polygon(arcpy.Array(i),SR)
    polygons.append(arr)
  if replace:
    if arcpy.Exists(output_shp):
      arcpy.Delete_management(output_shp)
  if union:
    polygons = union_poly(polygons)
  arcpy.CopyFeatures_management(polygons, output_shp)
  arcpy.CalculateField_management(output_shp,"Id","!FID!","PYTHON_9.3")
  del polygons,arr
import arcpy
import os
import sys
script = sys.argv[0]
path = (os.path.dirname(script)).replace("\\","/") + "/Shapefiles/"
#path = 'c:/temp/Shapefiles/'           # dump to here
print "\nRunning", script
arcpy.env.overwriteOutput = True
SR = arcpy.SpatialReference(3395)  # PCS 'WGS_1984_World_Mercator'
# Make rings.........................................................
X = [0,0,10,10,0]        # X,Y values for a square 10x10 units
Y = [0,10,10,0,0]
X_in = [1,1,-1,-1,1]     # inner buffer X, Y values
Y_in = [1,-1,-1,1,1]
XY = np.array(zip(X,Y))          # an XY array from zipped X,Y pairs
XY_in = np.array(zip(X_in,Y_in)) # buffer in... by distance
nose = np.array([[4,4],[5,6],[6,4],[4,4]])  # a triangle
p0 = [arcpy.Point(*pair) for pair in XY]  # root polygon points .....
XY1 = XY + [10,0]  # origin at 10,0
p1 = [arcpy.Point(*pair) for pair in XY1] # first feature with rings
p1a= [arcpy.Point(*pair) for pair in XY1 + XY_in]
p1b = [arcpy.Point(*pair) for pair in XY1 + (XY_in*2)]
p1c = [arcpy.Point(*pair) for pair in XY1 + (XY_in*3)]
p1d = [arcpy.Point(*pair) for pair in nose + [10,0]]
XY2 = XY + [20,0]  # origin at 20,0
p2 = [arcpy.Point(*pair) for pair in XY2] # second feature with rings
p2a= [arcpy.Point(*pair) for pair in (XY2 + XY_in)]
p2b = [arcpy.Point(*pair) for pair in (XY2 + (XY_in*2))]
p2c = [arcpy.Point(*pair) for pair in (XY2 + (XY_in*3))]
p2d = [arcpy.Point(*pair) for pair in (nose + [20,0])]
XY3 = XY + [30,0]  # origin at 30,0
p3 = [arcpy.Point(*pair) for pair in XY3] # second feature with rings
p3a= [arcpy.Point(*pair) for pair in (XY3 + XY_in)]
p3b = [arcpy.Point(*pair) for pair in (XY3 + (XY_in*2))]
p3c = [arcpy.Point(*pair) for pair in (XY3 + (XY_in*3))]
p3d = [arcpy.Point(*pair) for pair in (nose + [30,0])]
XY4 = XY + [0,10]
p4 = [arcpy.Point(*pair) for pair in XY4 ]
p4a = [arcpy.Point(*pair) for pair in (XY4 + XY_in)]
p4b = [arcpy.Point(*pair) for pair in (XY4 + (XY_in*2))]
p4c = [arcpy.Point(*pair) for pair in (XY4 + (XY_in*3))]
p4d = [arcpy.Point(*pair) for pair in nose + [0,10]]
p5a = [arcpy.Point(*pair) for pair in (XY + [10,10])]
p5b = [arcpy.Point(*pair) for pair in (XY + [20,20])]
p5c = [arcpy.Point(*pair) for pair in (XY + [30,10])]
p6a = [arcpy.Point(*pair) for pair in (XY + [10,20])]
p6b = [arcpy.Point(*pair) for pair in (XY + [20,10])]
p6c = [arcpy.Point(*pair) for pair in (XY + [30,20])]
# Make points........................................................
# comment out individual shapes that you don't want to see
output_shp = path + "x0.shp"    # ....the base polygon
rings = [p0]
polygonize(rings,output_shp,SR,False,True)
output_shp = path + "x1.shp"    # ....yields 3 seperate donut polygon
rings = [p1+p1a,p1b+p1c,p1d]
polygonize(rings,output_shp,SR,False,True)
output_shp = path + "x2.shp"    # same as above but with 'five' records
rings = [p2+p2a,p2a+p2b,p2b+p2c,p2c+p2d,p2d+p2d]  # make the donut plus rings
polygonize(rings,output_shp,SR,False,True)        # interesting
output_shp = path + "x3.shp"    # stacked polygon, same
rings = [p3,p3a,p3b,p3c,p3d]
polygonize(rings,output_shp,SR,False,True)
output_shp = path + "x4.shp"   # just the donut holes as 3 separate polygon
rings = [p4a+p4b,p4c+p4d]
polygonize(rings,output_shp,SR,False,True)
output_shp = path + "x5.shp"    # single part polygons
rings = [p5a,p5b,p5c]
polygonize(rings,output_shp,SR,False,True)
output_shp = path + "x6.shp"    # multi-part polygon
rings = [p6a,p6b,p6c]
polygonize(rings,output_shp,SR,True,True)

[DarrenWiens2]

Dan, you seem to have a handle on this - is Xander's polygon "flattened" (dissolved) at the call to create the polygon ("polygon= arcpy.Polygon(array)"), or elsewhere?

edit: I tried your script and it does not seem to address Xander's problem, specifically creating one multipart polygon containing shared edges.

[XanderBakker]

Hi Dan Patterson‌, thanks for posting the code. I adapted my code to create the list of rings

ring_list = [[arcpy.Point(float(pnt[0]), float(pnt[1])) for pnt in part] for part in mp]

out_shp = r"D:\Xander\GeoNet\MultiPart\shp\test02.shp"
polygonize(ring_list, out_shp, union=True)

... included your two defs in my code and gave it a shot...

I tried with union=True and union=False, but both cases don't give me the multipart feature with all the square parts in it.

So I thought, maybe I should use your data and see if that changes things. I ran your code (include import numpy as np) and I like the result.

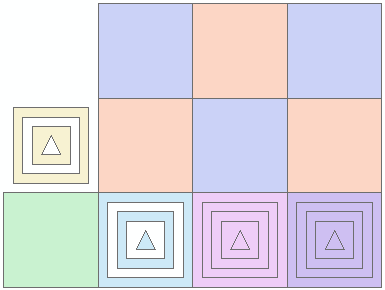
However, non of the cases describes what I'm looking for. So I added two cases:

• taking the 6 blueish + orange squares and process them with union
• and without union

output_shp = path + "x7.shp"    # multi-part polygon 2
rings = [p5a,p5b,p5c,p6a,p6b,p6c]
polygonize(rings,output_shp,SR,True,True)

output_shp = path + "x8.shp"    # single part polygons 2
rings = [p5a,p5b,p5c,p6a,p6b,p6c]
polygonize(rings,output_shp,SR,False,True)

The result is not what I am looking for (a multipart feature containing the 6 parts not dissolved into a single part polygon):

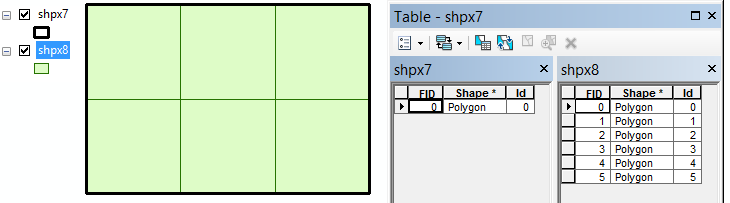
I am going to test on another version (10.1) to see if this may be due to my current version (10.3.0.4322)...

[DarrenWiens2 · Accepted solution]

Xander, I believe you are hitting a limitation regarding multipart geometry, not arcpy, outlined here‌ (although I could have sworn I've seen such multipart polygons before):

Keep in mind that parts in a multipart polygon are spatially separated. They can touch each other at vertices, but they cannot share edges or overlap. When you are sketching a multipart polygon, any parts that share an edge will be merged into a single part when you finish the sketch. In addition, any overlap among parts will be removed, leaving a hole in the polygon.

[XanderBakker]

Thanks Darren Wiens‌,

That would explain for this to happen (just a little too much intelligence when the polygon object is created). I wonder if I would move the polygons a tiny little fraction if this would create the multipart polygon...

Would be great to have an additional parameter "TurnYourBeatifulMultipartPolygonIntoOneDissolvedSinglepartPolygonAndRuinYourWork" in the polygon creation, which one could optionally set to False...

[XanderBakker]

Did a little test moving the squares a little with some increment and obtained this "beautiful" result:

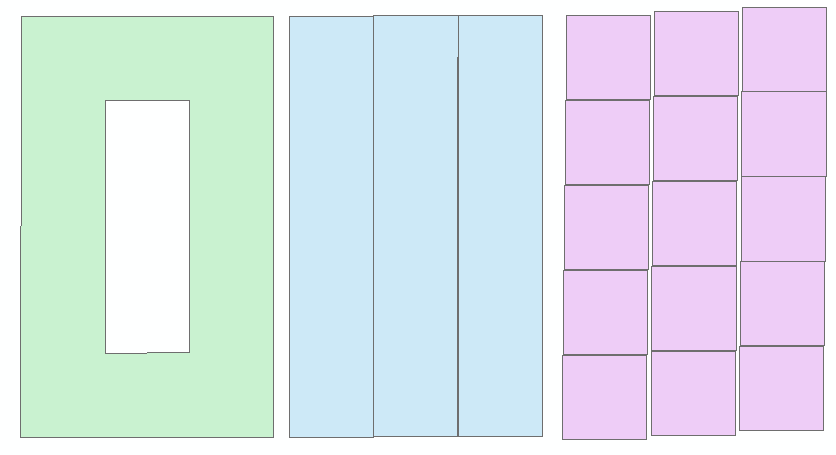
On the left little movement, in the middle a multipart with 3 parts was created (vertically dissolved the squares) and to the right a multipart with 15 parts was created. I suppose the XY tolerance for the data or defined in the environment setting also influences the result.

That confirms what Darren Wiens‌ was stating: "any parts that share an edge will be merged into a single part"...

[JoshuaBixby]

Darren Wiens you are correct in that it isn't an ArcPy limitation.  In fact, it isn't even an ArcGIS or Esri limitation, per se.  The quote from the Help link you provide is basically Esri paraphrasing an OGC standard without attribution or providing the 'why' to the user.

The OGC Simple Feature Access - Part 1: Common Architecture document clearly states the "boundaries of any 2 Polygons that are elements of a MultiPolygon may not 'cross' and may touch at only a finite number of Points," i.e., parts of a multipart polygon can't share an edge.  MultiLineStrings can have shared lines or lines on top of each other.  The Esri Knowledge Base article FAQ:  Why are polygon features grouped into multi-line string features by the ArcSDE sdegroup comman... speaks to this issue.

In short, the standard doesn't allow for it.  Esri implements the standard, and their way of staying compliant is to dissolve parts of multipart polygons that share edges.  Microsoft implements the standard as well, but their way of handling the situation in SQL Server is to let the user create an invalid polygon and then let it err out later when someone tries to work with the geometry.  Same standard, two different products, and two different ways of coping with a user creating an invalid multipart polygon.

[DanPatterson_Retired]

Ahh good catch...since I was trying to confirm that remained separate when they share a single node as in the case of my original multipart shape...if it is handled wrong, then you end up with the weird polygon output I was alluding to.  Great summary..and to note that moving them apart, dissolving, unioning and moving back doesn't work either I tried that with limited to no success when repair geometry was run on the resultant.

[DanPatterson_Retired]

Guys.... can I referenc Xander's example and Darren's comments?  I want should really update that blog post to include it, if that is ok with both of you.

And to put a bug into your ear.  I have recently been looking at 3D shape and I will have to see whether ArcMap includes the Z or M values when it does the dissolve ... consider two adjacent squares, square 1 has a Z value of 1.0, the second has a value of 1.1, they share edges, if turned into mulipart, is the Z (or M) considered...couldn't find anything on that, I know corners is OK.

if I finish that soon, I will post back here as well.