- Home
- :
- All Communities
- :
- Developers
- :
- Python
- :
- Python Questions
- :
- Re: Calculating "best fit" line feature based on t...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Calculating "best fit" line feature based on three height values
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi
I have line features representing overhead power lines, and for these power lines, I have height attribute values at three different locations: the start of the line, the end of the line and (using a distance attribute from start) the point of maximal sag of the line between start and end points. I do not want to create straight lines between start point, sag point and end point but a curved line of best fit between the three points. Note that the "sag" point is not always midway between the start and end point. I need to do this in a python program as I have to calculate this for a large volume of lines, so the editing "arc" tool is not really something I can use.
I looked into trying to fit an ellipsoid between the points but that is no good as this would mean I have one ellipsoid between start point and sag point and another ellipsoid between sag point and end point. I need a single curve that fits all three points. I tried the spline tool, which creates a raster surface from points (which means I can perhaps get back from raster to more points), but 3 points is not enough to create a raster surface. I also tried non spatial tools such as scipy interpolate (fitting a spline between sets of np.array values), but here also, I only have 3 points which is not sufficient to do the interpolation and create the "spline" line.
Anyone knows how to create a curve of best fit between three point locations? In my case these points are z (height) values so either a curved "best fit" line is calculated directly or intermediate points are calculated from which I create a new line feature. However, in that case I also would have to find the X and Y coordinates of the newly created (intermediate) z height values.
Difficult problem, I know, I am just wondering if someone has worked this out, or can help me in any way.
Thanks very much.
Hugo
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
We will have to await for Hugo Bouckaert to get back to us
... sort of retired...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
ah! sorry i thought i was replying to Hugo, but didn't look close enough! Cheers!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi Dan and Cody
Come to think of it, I suppose what I am really after is the ability (1) to draw this line in 3D space with XYZ coordinates and (2) to be able to calculate new Z locations given the input of a set distance from the start location. These two things are actually quite similar in the sense that drawing a sag line in 3D would require XYZ vertices along the way which also amounts to calculating the new Z values along the line. Any way this is achievable? Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
That bit of code looks good indeed! I am plugging it into Jupyter and substituting some of my own data to see if this comes out OK. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi Scott
Thanks for that. Yes I have data that more or less comply with what you are asking for, but also some extra information (see columns below). I have added in your field names and made red the columns I think correspond to yours above.
Note however that I did not have a distance "sag to end" so I took horizontal distance and subtracted "distance to max sag" from that, which should be the sag point to end point distance. I also do not have a separate "end z" field, but let's assume for now that it's z height is the same as the start z. So in the data below, I simply copied the column from start z.

Thanks
Hugo
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I'm pretty sure your data is indicating you have different elevations on either end, otherwise the distance to the sag would be in the middle of the curve.
As a quick thought (this will need tweaking)
For graphs with different elevations your basically solving the left side then the right side.
For each side you're going to figure out what the curve scale is (from function provided)
Calculate Z difference from Start Z to Sag Z
Calculate the distance between start XY and sag XY (this you should already have based on your table)
Solve left side using above as inputs. Lets call it L_CURVE_VALUE
Determine the XY locations between the start and mid point (something like np.linspace for each of the X and Y should give you a sufficiently density of array of values for your curve).
For example lets say you get 100 points between the start and sag
Given that your Sag point XY is 0, use something like np.linspace to create array of points from 0 to your distance (start to sag). Use same number of points as XY locations above. lets call this Z_map
Plug that Z_map into the formula ((L_CURVE_VALUE * np.cosh(Z_map/L_CURVE_VALUE)) - L_CURVE_VALUE)
this is the array of the curve Z points based on your inputs. Let call this Z_TABLE
Add the Sag Z elevation to the Z_TABLE. This will put it into your proper vertical location, otherwise it would be Z values from 0 to N (being the start elevation). Call this Z_Locations
Repeat for other side (using different variables for X, Y, Z locations).
Join left side and right side locations together (making sure it goes from Start to Sag, Sag to End in your arrays).
use these as inputs in the arcpy.polyline when creating a new line between points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi Cody
Thanks for that. Given that in the above code we have the function def solve_eq, I did this what you suggested in the main body of the code. But surely this can't be right as I am getting an error that it needs a float whereas I am using a tuple for Z_map. Do I have to pass the array values in one by one? I have highlighted what I have done in bold. The values for Z_map are:
(array([50. , 48.75, 47.5 , 46.25, 45. ]), -1.25)
# This is the input:
dd = [[10, 10, 50, 45, 50]]
lx = None
ly = None
rx = None
ry = None
for i in dd:
dist_1 = i[0]
sag_1 = i[2]-i[3]
a_1 = solve_eq(sag_1, dist_1, max_decimals=10)
dist_2 = i[1]
sag_2 = i[4]-i[3]
a_2 = solve_eq(sag_2, dist_2, max_decimals=10)
lx = np.linspace(-i[0], 0)
ly = ((a_1 * np.cosh(lx/a_1))-a_1) + i[3]
Z_map = np.linspace(10, 45, num=5, retstep=True)
# ((L_CURVE_VALUE * np.cosh(Z_map/L_CURVE_VALUE)) - L_CURVE_VALUE)
ly2 = ((a_1 * np.cosh(Z_map/a_1)) - a_1)
print ('ly2 is {0}'.format(ly2))
ly = np.clip(ly, i[3], i[2])
print ('ly is {0}'.format(ly))
rx = np.linspace(0, i[1])
ry = ((a_2 * np.cosh(rx/a_2))-a_2) + i[3]
ry = np.clip(ry, i[3], i[4])
fig, ax = plt.subplots(1,1, figsize=(20, 10))
ax.plot(lx, ly)
ax.plot(rx, ry)
ax.grid()
Thanks
Hugo
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Heres what i was thinking: You'll also need the solve_eq from the previous work
from collections import namedtuple
def calculate_xy_path(_start, _end, _sag, density=None):
l_x = np.linspace(_start.x, _sag.x, density)
r_x = np.linspace(_sag.x, _end.x, density)
l_y = np.linspace(_start.y, _sag.y, density)
r_y = np.linspace(_sag.y, _end.y, density)
l_z = calculate_z_path(_start, _sag, density)[::-1]
r_z = calculate_z_path(_sag, _end, density)
return Path(x=l_x, y=l_y, z=l_z), Path(x=r_x, y=r_y, z=r_z)
def calculate_z_path(_start, _end, density):
distance = math.sqrt(((_start.x - _end.x)**2) + ((_start.y - _end.y)**2))
sag_value = abs(_start.z - _end.z)
bottom_value = min(_start.z, _end.z)
_path = np.linspace(0, distance, density)
c = solve_eq(sag_value, distance, max_decimals=3)
_z_path = ((c * np.cosh(_path/c))-c)
_z_path = np.clip(_z_path, 0, sag_value)
return _z_path + bottom_value
Point = namedtuple("Point", "x y z")
Path = namedtuple("Path", "x y z")
start_point = Point(x=300, y=300, z=50)
end_point = Point(x=400, y=400, z=50)
sag_point = Point(x=350, y=350, z=40)
left_path, right_path = calculate_xy_path(start_point, end_point, sag_point, 20)
full_path = Path(
x=np.concatenate((left_path.x, right_path.x)),
y=np.concatenate((left_path.y, right_path.y)),
z=np.concatenate((left_path.z, right_path.z))
)Then to test plot
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111, projection='3d')
ax.plot(full_path.x, full_path.y, full_path.z)
for p in [start_point, sag_point, end_point]:
ax.scatter([p.x], [p.y], [p.z], c='r')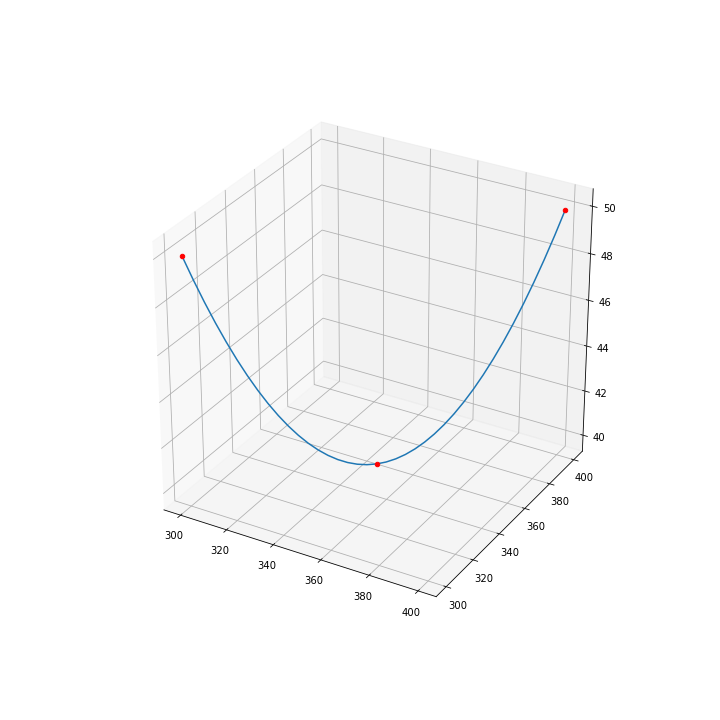
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Thanks a million Cody, appreciated, this looks like it is going to work. I will definitely try this out on my data!
Cheers
Hugo
- « Previous
-
- 1
- 2
- Next »
- « Previous
-
- 1
- 2
- Next »