- Home
- :
- All Communities
- :
- Products
- :
- Geoprocessing
- :
- Geoprocessing Questions
- :
- Create new feature point at minimum distance betwe...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Create new feature point at minimum distance between numerous points
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Is there a tool or workflow that can create a feature at minimum distance or equal distance between several points? This is a general question but to clarify I've attached a couple images to show what I mean with three points:
Below are a couple candidate points:

Here I've created a some Thiessen Polygons:
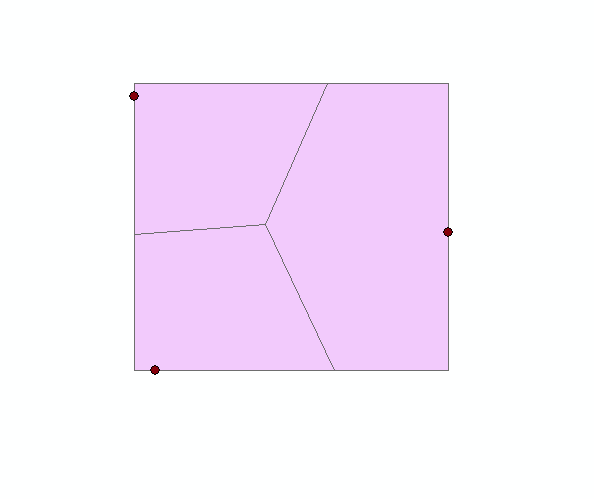
Then I convert the vertices of the Thiessen polygons to points and select the point at the center:
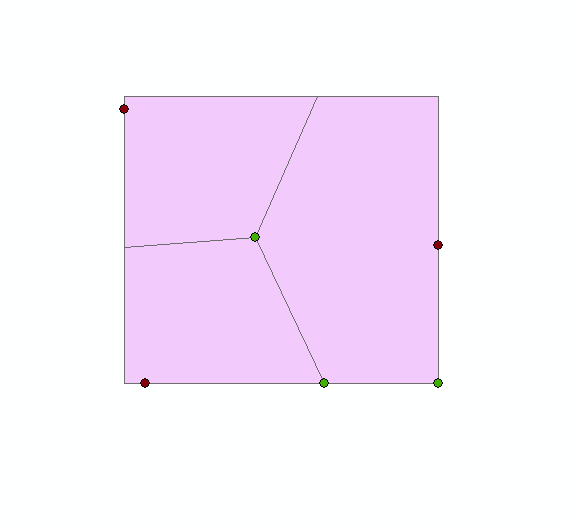
This is just a simple example of what I'd like to learn how to do on a larger scale, e.g. to create more than one "minimum distance" points over an area containing a lot more candidate points. The goal is to automate this as well so the user doesn't have to go in and select the points located between the desired points and omit those on the edge.
Any thoughts, advice, or references to similar posts would be greatly appreciated. Thanks!
Case
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
You could use CreateRandomPoints and specify minimum_allowed_distance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
There is also code in my GitHub that does similar assurances of n points not spaced closer than some threshold.
You could create your own tool from the def if you wanted to.
It uses a complete random generation of points per cycle, this may differ from what esri's tool that Steve references (it isn't documented)
EDIT
It only requires a Basic license and no SA or 3D... you just need numpy installed, which isn't a problem with new versions of ArcMap
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Thanks Dan, I will check that out. Should it be a concern that I'm not looking to set a specific distance but simply the minimum travel distance with the tool you're referencing?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I will play with the CreateRandomPoints tool but I'm not looking to restrict the distance to a specific value but rather the minimum distance between points. To give more context, I have a tool that outputs several candidate polygons, creates a point for their centroids, and then I'd like to create a new feature point between the centroids.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
So to clarify, you essentially want to build a sequence or net of equilateral triangles then? (just to rule out a fishnet conversion to points ... since the diagonal wouldn't be equally spaced)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I believe so, yes. I was going to establish a fishnet grid over my study area and simply select equidistant points from it but I'm not sure that would get the results I'd like in all scenarios, however that's what I am experimenting with now.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Fishnet converted to points is an obvious candidate... there are several incarnations of hexagon generation on GeoNet... another candidate
I guess when you decide on a structure for your point patterns, it will be easy to generate what you need. It is just your all points must be equally spaced only gives you the option of points on an equilateral triangle... even an isosceles or scalene isn't going to cut it, let alone any other regular geometry configuration.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Thanks, that gives me some to work with and experiment. Just out of curiosity, in your experience have Thiessen polygons been employed in a similar context that a regularly spaced grid (fishnet or hexagon) have proven useful? I need look into the math for Thiessen polygons since it's been a while but I wonder if their are any constraints that could be used to develop a TIN type grid for minimum distance or optimizing point selection. Thanks again for the help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
a Delaunay triangulation is the basis for a TIN... it connects points such that the circle formed by those points contains no other points. It is another way of delineating space, and its 'dual' (aka sibling) is the Voronoi diagram. Theissen is just another name, more often associated with climatologists... In short, you either connect the dots or form areas around the dots, but the guiding circle ensures everything behaves as designed