Community

Formula For State Plane to Lat/Lon Conversion

55337
24
08-07-2014 10:20 AM
GeorgePorto
by
Occasional Contributor
‎08-07-2014 10:20 AM

Does anyone know where I can find the equation to put into Excel that will convert CT State Plane coordinates to Lat/Lon?  I know ways to programmatically do this using ArcGIS but have a scenario/workflow where we may need to do this from within Excel.  Thanks!

24 Replies
ThomasMarshall
by
New Contributor
‎02-24-2017 12:52 PM

I would very much like a copy of your SQL formulas. I once tried to do this using SQL, but due to the large numbers of formulas involved,and the number of steps, I found that rounding errors became significant, and my results were not as accurate as I needed.

If you have found a better way, I would be very interested.

0 Kudos
mpboyle
by
Frequent Contributor
‎02-24-2017 01:47 PM

Thomas Marshall‌

Since I can't attach through a comment, below are the Sql functions, and some notes to be aware of...

  • These functions calculate longitude and latitude for Lambert Conformal Conic 2-parallel projections (as this is what our production features are stored in (wkid: 6463 --- NAD 1983 (2011) Iowa State Plane North))
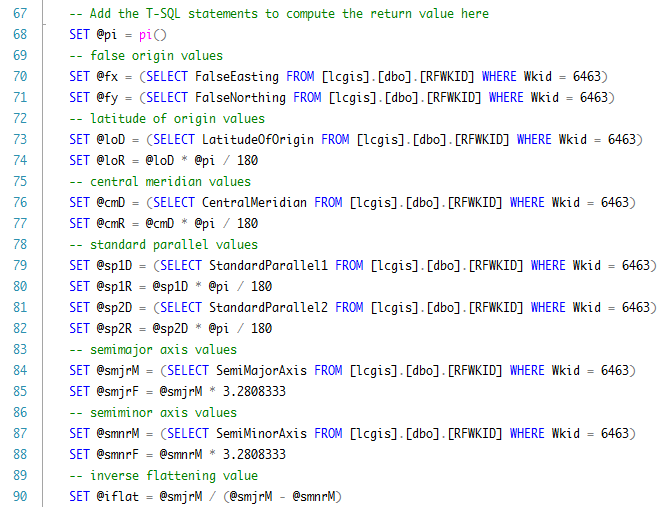
  • Note lines 59 through 76 --- you will need to provide the values for your coordinate system
    • You can find these values within the XY Coordinate System  properties of a feature class
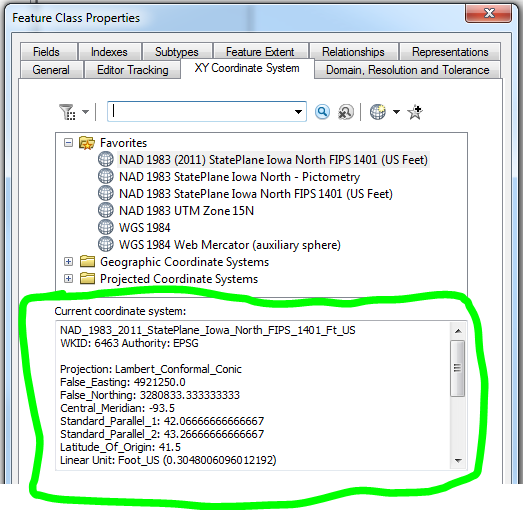
    • I do this by storing the values in a table and call them through a SELECT statement, that way the values are stored in one place (example below)

Longitude Calculation

USE [**DatabaseName**]
GO
/****** Object:  UserDefinedFunction [dbo].[get_longitude] ******/
SET ANSI_NULLS ON
GO
SET QUOTED_IDENTIFIER ON
GO
-- =============================================
-- Author:     Your Name
-- Create date: Date
-- Description:     Returns longitude given x,y coordinates in Lambert Conformal Conic projection
-- =============================================
CREATE FUNCTION [dbo].[get_longitude] 
(
     -- Add the parameters for the function here
     @x numeric(24,12),  --state plane x coordinate
     @y numeric(24,12)   --state plane y coordinate
)
RETURNS numeric(24,12)
AS
BEGIN
     -- Declare the return variable here
   DECLARE
   @pi numeric(24,12),     --pi
   @fx numeric(24,12),     --false easting
   @fy numeric(24,12),     --false northing
   @cmD numeric(24,12),    --central meridian in degrees
   @cmR numeric(24,12),    --central meridian in radians
   @sp1D numeric(24,12),   --standard parallel 1 in degrees
   @sp1R numeric(24,12),   --standard parallel 1 in radians
   @sp2D numeric(24,12),   --standard parallel 2 in degrees
   @sp2R numeric(24,12),   --standard parallel 2 in radians
   @loD numeric(24,12),    --latitude of origin in degrees
   @loR numeric(24,12),    --latitude of origin in radians
   @smjrM numeric(24,12),  --semimajor axis in meters
   @smjrF numeric(24,12),  --semimajor axis in feet
   @smnrM numeric(24,12),  --semiminor axis in meters
   @smnrF numeric(24,12),  --semiminor axis in feet
   @flat numeric(24,12),   --flattenging
   @iflat numeric(24,12),  --inverse flattening
   @e numeric(24,12),      --eccentricity
   @m1 numeric(24,12),     --calculation value
   @m2 numeric(24,12),     --calculation value
   @t1 numeric(24,12),     --calculation value
   @t2 numeric(24,12),     --calculation value
   @tf numeric(24,12),     --calculation value
   @n numeric(24,12),      --calculation value
   @F numeric(24,12),      --calculation value
   @rf numeric(24,12),     --calculation value
   @rz numeric(24,12),     --calculation value
   @tz numeric(24,12),     --calculation value
   @zz numeric(24,12),     --calculation value
   @lonR numeric(24,12),   --longitude in radians
   @lonD numeric(24,12)    --longitude in degrees

   -- Add the T-SQL statements to compute the return value here
   SET @pi = pi()
   -- false origin values
   SET @fx = /* Enter false easting value */
   SET @fy = /* Enter false northing value */
   -- latitude of origin values
   SET @loD = /* Enter latitude of origin value */
   SET @loR = @loD * @pi / 180
   -- central meridian values
   SET @cmD = /* Enter central meridian value */
   SET @cmR = @cmD * @pi / 180
   -- standard parallel values
   SET @sp1D = /* Enter standard parallel 1 value */
   SET @sp1R = @sp1D * @pi / 180
   SET @sp2D = /* Enter standard parallel 2 value */
   SET @sp2R = @sp2D * @pi / 180
   -- semimajor axis values
   SET @smjrM = /* Enter semimajor axis value in meters */
   SET @smjrF = @smjrM * 3.2808333
   -- semiminor axis values
   SET @smnrM = /* Enter semiminor axis value in meters */
   SET @smnrF = @smnrM * 3.2808333
   -- inverse flattening value
   SET @iflat = @smjrM / (@smjrM - @smnrM)
   -- flattenging value
   SET @flat = 1 / @iflat
   -- eccentricity value
   SET @e = SQRT(2 * @flat - SQUARE(@flat))
   -- m values
   SET @m1 = COS(@sp1R) / POWER((1 - SQUARE(@e) * SQUARE(SIN(@sp1R))), 0.5)
   SET @m2 = COS(@sp2R) / POWER((1 - SQUARE(@e) * SQUARE(SIN(@sp2R))), 0.5)
   -- t values
   SET @t1 = TAN((@pi / 4) - (@sp1R / 2)) / POWER((1 - (@e * SIN(@sp1R))) / (1 + (@e * SIN(@sp1R))), (@e / 2))
   SET @t2 = TAN((@pi / 4) - (@sp2R / 2)) / POWER((1 - (@e * SIN(@sp2R))) / (1 + (@e * SIN(@sp2R))), (@e / 2))
   SET @tf = TAN((@pi / 4) - (@loR / 2)) / POWER((1 - (@e * SIN(@loR))) / (1 + (@e * SIN(@loR))), (@e / 2))
   -- n value
   SET @n = (LOG(@m1) - LOG(@m2)) / (LOG(@t1) - LOG(@t2))
   -- f value
   SET @F = @m1 / (@n * POWER(@t1, @n))
   -- r value
   SET @rf = @smjrF * @F * POWER(@tf, @n)
   -- r' value
   SET @rz = POWER(POWER((@x - @fx), 2) + POWER((@rf - (@y - @fy)), 2), 0.5)
   -- t' value
   SET @tz = POWER((@rz / (@smjrF * @F)), (1 / @n))
   -- thetha' value
   SET @zz = ATAN((@x - @fx) / (@rf - (@y - @fy)))
   -- longitude value in radians
   SET @lonR = ((@zz / @n) + @cmR)
   -- longitude value in degrees
   SET @lonD = (@lonR * 180) / @pi

     -- Return the result of the function
     RETURN @lonD;

END
‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍

Latitude Calculation

USE [**DatabaseName**]
GO
/****** Object:  UserDefinedFunction [dbo].[get_latitude] ******/
SET ANSI_NULLS ON
GO
SET QUOTED_IDENTIFIER ON
GO
-- =============================================
-- Author:     Your Name
-- Create date: Date
-- Description:     Returns latitude given x,y coordinates in Lambert Conformal Conic projection
-- =============================================
CREATE FUNCTION [dbo].[get_latitude] 
(
     -- Add the parameters for the function here
     @x numeric(24,12),  --state plane x coordinate
     @y numeric(24,12)   --state plane y coordinate
)
RETURNS numeric(24,12)
AS
BEGIN
     -- Declare the return variable here
   DECLARE
   @pi numeric(24,12),     --pi
   @fx numeric(24,12),     --false easting
   @fy numeric(24,12),     --false northing
   @cmD numeric(24,12),    --central meridian in degrees
   @cmR numeric(24,12),    --central meridian in radians
   @sp1D numeric(24,12),   --standard parallel 1 in degrees
   @sp1R numeric(24,12),   --standard parallel 1 in radians
   @sp2D numeric(24,12),   --standard parallel 2 in degrees
   @sp2R numeric(24,12),   --standard parallel 2 in radians
   @loD numeric(24,12),    --latitude of origin in degrees
   @loR numeric(24,12),    --latitude of origin in radians
   @smjrM numeric(24,12),  --semimajor axis in meters
   @smjrF numeric(24,12),  --semimajor axis in feet
   @smnrM numeric(24,12),  --semiminor axis in meters
   @smnrF numeric(24,12),  --semiminor axis in feet
   @flat numeric(24,12),   --flattenging
   @iflat numeric(24,12),  --inverse flattening
   @e numeric(24,12),      --eccentricity
   @m1 numeric(24,12),     --calculation value
   @m2 numeric(24,12),     --calculation value
   @t1 numeric(24,12),     --calculation value
   @t2 numeric(24,12),     --calculation value
   @tf numeric(24,12),     --calculation value
   @n numeric(24,12),      --calculation value
   @F numeric(24,12),      --calculation value
   @rf numeric(24,12),     --calculation value
   @rz numeric(24,12),     --calculation value
   @tz numeric(24,12),     --calculation value
   @zz numeric(24,12),     --calculation value
   @latTR numeric(24,12),  --latitude trial in radians
   @lat1R numeric(24,12),  --latitude iteration 1 in radians
   @lat2R numeric(24,12),  --latitude iteration 2 in radians
   @lat3R numeric(24,12),  --latitude iteration 3 in radians
   @lat4R numeric(24,12),  --latitude iteration 4 in radians
   @latFR numeric(24,12),  --latitude final iteration in radians
   @latTD numeric(24,12),  --latitude trial in degrees
   @lat1D numeric(24,12),  --latitude iteration 1 in degrees
   @lat2D numeric(24,12),  --latitude iteration 2 in degrees
   @lat3D numeric(24,12),  --latitude iteration 3 in degrees
   @lat4D numeric(24,12),  --latitude iteration 4 in degrees
   @latFD numeric(24,12)   --latitude final iteration in degrees


   -- Add the T-SQL statements to compute the return value here
   SET @pi = pi()
   -- false origin values
   SET @fx = /* Enter false easting value */
   SET @fy = /* Enter false northing value */
   -- latitude of origin values
   SET @loD = /* Enter latitude of origin value */
   SET @loR = @loD * @pi / 180
   -- central meridian values
   SET @cmD = /* Enter central meridian value */
   SET @cmR = @cmD * @pi / 180
   -- standard parallel values
   SET @sp1D = /* Enter standard parallel 1 value */
   SET @sp1R = @sp1D * @pi / 180
   SET @sp2D = /* Enter standard parallel 2 value */
   SET @sp2R = @sp2D * @pi / 180
   -- semimajor axis values
   SET @smjrM = /* Enter semimajor axis value in meters */
   SET @smjrF = @smjrM * 3.2808333
   -- semiminor axis values
   SET @smnrM = /* Enter semiminor axis value in meters */
   SET @smnrF = @smnrM * 3.2808333
   -- inverse flattening value
   SET @iflat = @smjrM / (@smjrM - @smnrM)
   -- flattenging value
   SET @flat = 1 / @iflat
   -- eccentricity value
   SET @e = SQRT(2 * @flat - SQUARE(@flat))
   -- m values
   SET @m1 = COS(@sp1R) / POWER((1 - SQUARE(@e) * SQUARE(SIN(@sp1R))), 0.5)
   SET @m2 = COS(@sp2R) / POWER((1 - SQUARE(@e) * SQUARE(SIN(@sp2R))), 0.5)
   -- t values
   SET @t1 = TAN((@pi / 4) - (@sp1R / 2)) / POWER((1 - (@e * SIN(@sp1R))) / (1 + (@e * SIN(@sp1R))), (@e / 2))
   SET @t2 = TAN((@pi / 4) - (@sp2R / 2)) / POWER((1 - (@e * SIN(@sp2R))) / (1 + (@e * SIN(@sp2R))), (@e / 2))
   SET @tf = TAN((@pi / 4) - (@loR / 2)) / POWER((1 - (@e * SIN(@loR))) / (1 + (@e * SIN(@loR))), (@e / 2))
   -- n value
   SET @n = (LOG(@m1) - LOG(@m2)) / (LOG(@t1) - LOG(@t2))
   -- f value
   SET @F = @m1 / (@n * POWER(@t1, @n))
   -- r value
   SET @rf = @smjrF * @F * POWER(@tf, @n)
   -- r' value
   SET @rz = POWER(POWER((@x - @fx), 2) + POWER((@rf - (@y - @fy)), 2), 0.5)
   -- t' value
   SET @tz = POWER((@rz / (@smjrF * @F)), (1 / @n))
   -- thetha' value
   SET @zz = ATAN((@x - @fx) / (@rf - (@y - @fy)))
   -- latitude trial value in radians
   SET @latTR = (@pi / 2) - (2 * ATAN(@tz))
   -- latitude iteration 1 value in radians
   SET @lat1R = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@latTR))) / (1 + (@e * SIN(@latTR))), (@e / 2)))))
   -- latitude iteration 2 value in radians
   SET @lat2R = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@lat1R))) / (1 + (@e * SIN(@lat1R))), (@e / 2)))))
   -- latitude iteration 3 value in radians
   SET @lat3R = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@lat2R))) / (1 + (@e * SIN(@lat2R))), (@e / 2)))))
   -- latitude iteration 4 value in radians
   SET @lat4R = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@lat3R))) / (1 + (@e * SIN(@lat3R))), (@e / 2)))))
   -- latitude final iteration value in radians
   SET @latFR = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@lat4R))) / (1 + (@e * SIN(@lat4R))), (@e / 2)))))
   -- latitude trial value in degrees
   SET @latTD = (@latTR * 180) / @pi
   -- latitude iteration 1 value in degrees
   SET @lat1D = (@lat1R * 180) / @pi
   -- latitude iteration 2 value in degrees
   SET @lat2D = (@lat2R * 180) / @pi
   -- latitude iteration 3 value in degrees
   SET @lat3D = (@lat3R * 180) / @pi
   -- latitude iteration 4 value in degrees
   SET @lat4D = (@lat4R * 180) / @pi
   -- latitude final iteration value in degrees
   SET @latFD = (@latFR * 180) / @pi


     -- Return the latitude in degrees
     RETURN @latFD;

END
‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍‍
ThomasMarshall
by
New Contributor
‎02-24-2017 01:51 PM

I'll give it a try. Thanks!

0 Kudos
JohnHansen
by
Occasional Contributor
‎09-29-2017 03:41 PM

This is awesome - thanks so much.Works well, and very fast.

0 Kudos
MichaelMorgan4
by
Regular Contributor
‎05-18-2018 03:06 PM

Very helpful, thanks a million. I have to keep all my geographically projected feature classes in SQL Server for easy retrieval with other applications, and the ESRI Python script I thought I had to use just for reprojection kept crashing and burning on me.

0 Kudos
DrewDowling
by
Frequent Contributor
‎03-10-2021 09:09 AM

It looks like the last forum migration messed up the formatting of your code. I've reformatted it to maybe help others. Hope you don't mind.

USE yourDB
GO

/****** Object:  UserDefinedFunction [dbo].[get_longitude] ******/
SET ANSI_NULLS ON
GO
SET QUOTED_IDENTIFIER ON
GO
-- =============================================
-- Author:     Your Name
-- Create date: Date
-- Description:     Returns longitude given x,y coordinates in Lambert Conformal Conic projection
-- =============================================C
CREATE FUNCTION [dbo].[get_longitude] (     
        -- Add the parameters for the function here     
        @x numeric(24,12),  
        --state plane x coordinate     
        @y numeric(24,12)   
        --state plane y coordinate
    )
    RETURNS numeric(24,12)
    AS
    BEGIN     
        -- Declare the return variable here   
        DECLARE   @pi numeric(24,12),     
        --pi   
        @fx numeric(24,12),     
        --false easting   
        @fy numeric(24,12),     
        --false northing   
        @cmD numeric(24,12),    
        --central meridian in degrees   
        @cmR numeric(24,12),    
        --central meridian in radians   
        @sp1D numeric(24,12),   
        --standard parallel 1 in degrees   
        @sp1R numeric(24,12),   
        --standard parallel 1 in radians   
        @sp2D numeric(24,12),   
        --standard parallel 2 in degrees   
        @sp2R numeric(24,12),   
        --standard parallel 2 in radians   
        @loD numeric(24,12),    
        --latitude of origin in degrees   
        @loR numeric(24,12),    
        --latitude of origin in radians   
        @smjrM numeric(24,12),  
        --semimajor axis in meters   
        @smjrF numeric(24,12),  
        --semimajor axis in feet   
        @smnrM numeric(24,12),  
        --semiminor axis in meters  
        @smnrF numeric(24,12),  
        --semiminor axis in feet   
        @flat numeric(24,12),   
        --flattenging   
        @iflat numeric(24,12),  
        --inverse flattening   
        @e numeric(24,12),      
        --eccentricity   
        @m1 numeric(24,12),     
        --calculation value   
        @m2 numeric(24,12),     
        --calculation value   
        @t1 numeric(24,12),     
        --calculation value   
        @t2 numeric(24,12),     
        --calculation value   
        @TF numeric(24,12),     
        --calculation value   
        @n numeric(24,12),     
        --calculation value   
        @F numeric(24,12),     
        --calculation value   
        @RF numeric(24,12),    
        --calculation value  
        @RZ numeric(24,12),     
        --calculation value   
        @tz numeric(24,12),     
        --calculation value   
        @zz numeric(24,12),     
        --calculation value   
        @lonR numeric(24,12),   
        --longitude in radians   
        @lonD numeric(24,12)    
        --longitude in degrees   
        -- Add the T-SQL statements to compute the return value here   
        SET @pi = pi()   
        -- false origin values   
        SET @fx = /* Enter false easting value */   
        SET @fy = /* Enter false northing value */   
        -- latitude of origin values   
        SET @loD = /* Enter latitude of origin value */   
        SET @loR = @loD * @pi / 180   
        -- central meridian values   
        SET @cmD = /* Enter central meridian value */   
        SET @cmR = @cmD * @pi / 180   
        -- standard parallel values   
        SET @sp1D = /* Enter standard parallel 1 value */   
        SET @sp1R = @sp1D * @pi / 180   
        SET @sp2D = /* Enter standard parallel 2 value */   
        SET @sp2R = @sp2D * @pi / 180   
        -- semimajor axis values   
        SET @smjrM =  /* Enter semimajor axis value in meters */   
        SET @smjrF = @smjrM * 3.2808333   
        -- semiminor axis values   
        SET @smnrM =  /* Enter semiminor axis value in meters */   
        SET @smnrF = @smnrM * 3.2808333  
        -- inverse flattening value   
        SET @iflat = @smjrM / (@smjrM - @smnrM)   
        -- flattenging value   
        SET @flat = 1 / @iflat   
        -- eccentricity value   
        SET @e = SQRT(2 * @flat - SQUARE(@flat))   
        -- m values   
        SET @m1 = COS(@sp1R) / POWER((1 - SQUARE(@e) * SQUARE(SIN(@sp1R))), 0.5)   
        SET @m2 = COS(@sp2R) / POWER((1 - SQUARE(@e) * SQUARE(SIN(@sp2R))), 0.5)   
        -- t values   
        SET @t1 = TAN((@pi / 4) - (@sp1R / 2)) / POWER((1 - (@e * SIN(@sp1R))) / (1 + (@e * SIN(@sp1R))), (@e / 2))   
        SET @t2 = TAN((@pi / 4) - (@sp2R / 2)) / POWER((1 - (@e * SIN(@sp2R))) / (1 + (@e * SIN(@sp2R))), (@e / 2))   
        SET @TF = TAN((@pi / 4) - (@loR / 2)) / POWER((1 - (@e * SIN(@loR))) / (1 + (@e * SIN(@loR))), (@e / 2))   
        -- n value   
        SET @n = (LOG(@m1) - LOG(@m2)) / (LOG(@t1) - LOG(@t2))   
        -- f value   
        SET @F = @m1 / (@n * POWER(@t1, @n))   
        -- r value   
        SET @RF = @smjrF * @F * POWER(@tf, @n)   
        -- r' value   
        SET @RZ = POWER(POWER((@x - @fx), 2) + POWER((@rf - (@y - @fy)), 2), 0.5)   
        -- t' value   
        SET @tz = POWER((@rz / (@smjrF * @F)), (1 / @n))   
        -- thetha' value   
        SET @zz = ATAN((@x - @fx) / (@rf - (@y - @fy)))   
        -- longitude value in radians   
        SET @lonR = ((@zz / @n) + @cmR)   
        -- longitude value in degrees   
        SET @lonD = (@lonR * 180) / @pi     
        -- Return the result of the function     
        RETURN @lonD;
    END

 

 

USE yourDB
GO

/****** Object:  UserDefinedFunction [dbo].[get_latitude] ******/
SET ANSI_NULLS ON
GO
SET QUOTED_IDENTIFIER ON
GO

CREATE FUNCTION [dbo].[get_latitude] (  
      
        -- Add the parameters for the function here     
        @x numeric(24,12),  
        --state plane x coordinate     
        @y numeric(24,12)   
        --state plane y coordinate
    )
    RETURNS numeric(24,12)
        AS
    BEGIN
-- Declare the return variable here   
        DECLARE @pi numeric(24,12),
        --pi   
        @fx numeric(24,12),     
        --false easting   
        @fy numeric(24,12),     
        --false northing   
        @cmD numeric(24,12),    
        --central meridian in degrees   
        @cmR numeric(24,12),    
        --central meridian in radians   
        @sp1D numeric(24,12),   
        --standard parallel 1 in degrees   
        @sp1R numeric(24,12),   
        --standard parallel 1 in radians   
        @sp2D numeric(24,12),   
        --standard parallel 2 in degrees   
        @sp2R numeric(24,12),   
        --standard parallel 2 in radians   
        @loD numeric(24,12),    
        --latitude of origin in degrees   
        @loR numeric(24,12),    
        --latitude of origin in radians   
        @smjrM numeric(24,12),  
        --semimajor axis in meters   
        @smjrF numeric(24,12),  
        --semimajor axis in feet   
        @smnrM numeric(24,12),  
        --semiminor axis in meters   
        @smnrF numeric(24,12),  
        --semiminor axis in feet   
        @flat numeric(24,12),   
        --flattenging   
        @iflat numeric(24,12),  
        --inverse flattening   
        @e numeric(24,12),      
        --eccentricity   
        @m1 numeric(24,12),     
        --calculation value   
        @m2 numeric(24,12),     
        --calculation value   
        @t1 numeric(24,12),     
        --calculation value   
        @t2 numeric(24,12),     
        --calculation value   
        @TF numeric(24,12),     
        --calculation value   
        @n numeric(24,12),      
        --calculation value   
        @F numeric(24,12),      
        --calculation value   
        @RF numeric(24,12),     
        --calculation value   
        @RZ numeric(24,12),     
        --calculation value   
        @tz numeric(24,12),     
        --calculation value   
        @zz numeric(24,12),     
        --calculation value   
        @latTR numeric(24,12),  
        --latitude trial in radians   
        @lat1R numeric(24,12),  
        --latitude iteration 1 in radians   
        @lat2R numeric(24,12),  
        --latitude iteration 2 in radians   
        @lat3R numeric(24,12),  
        --latitude iteration 3 in radians   
        @lat4R numeric(24,12),  
        --latitude iteration 4 in radians   
        @latFR numeric(24,12),  
        --latitude final iteration in radians   
        @latTD numeric(24,12),  
        --latitude trial in degrees   
        @lat1D numeric(24,12),  
        --latitude iteration 1 in degrees   
        @lat2D numeric(24,12),  
        --latitude iteration 2 in degrees   
        @lat3D numeric(24,12),  
        --latitude iteration 3 in degrees   
        @lat4D numeric(24,12),  
        --latitude iteration 4 in degrees   
        @latFD numeric(24,12)   
        --latitude final iteration in degrees
        -- Add the T-SQL statements to compute the return value here
        SET @pi = pi()   
        -- false origin values   
        SET @fx =  /* Enter false easting value */   
        SET @fy =  /* Enter false northing value */   
        -- latitude of origin values   
        SET @loD =  /* Enter latitude of origin value */   
        SET @loR = @loD * @pi / 180   
        -- central meridian values   
        SET @cmD =  /* Enter central meridian value */   
        SET @cmR = @cmD * @pi / 180   
        -- standard parallel values   
        SET @sp1D =  /* Enter standard parallel 1 value */   
        SET @sp1R = @sp1D * @pi / 180   
        SET @sp2D =  /* Enter standard parallel 2 value */   
        SET @sp2R = @sp2D * @pi / 180   
        -- semimajor axis values   
        SET @smjrM =   /* Enter semimajor axis value in meters */   
        SET @smjrF = @smjrM * 3.2808333   
        -- semiminor axis values   
        SET @smnrM =  /* Enter semiminor axis value in meters */   
        SET @smnrF = @smnrM * 3.2808333   
        -- inverse flattening value   
        SET @iflat = @smjrM / (@smjrM - @smnrM)   
        -- flattenging value   
        SET @flat = 1 / @iflat   
        -- eccentricity value   
        SET @e = SQRT(2 * @flat - SQUARE(@flat))   
        -- m values   
        SET @m1 = COS(@sp1R) / POWER((1 - SQUARE(@e) * SQUARE(SIN(@sp1R))), 0.5)   
        SET @m2 = COS(@sp2R) / POWER((1 - SQUARE(@e) * SQUARE(SIN(@sp2R))), 0.5)   
        -- t values   
        SET @t1 = TAN((@pi / 4) - (@sp1R / 2)) / POWER((1 - (@e * SIN(@sp1R))) / (1 + (@e * SIN(@sp1R))), (@e / 2))   
        SET @t2 = TAN((@pi / 4) - (@sp2R / 2)) / POWER((1 - (@e * SIN(@sp2R))) / (1 + (@e * SIN(@sp2R))), (@e / 2))   
        SET @TF = TAN((@pi / 4) - (@loR / 2)) / POWER((1 - (@e * SIN(@loR))) / (1 + (@e * SIN(@loR))), (@e / 2))   
        -- n value   
        SET @n = (LOG(@m1) - LOG(@m2)) / (LOG(@t1) - LOG(@t2))   
        -- f value   
        SET @F = @m1 / (@n * POWER(@t1, @n))   
        -- r value   
        SET @RF = @smjrF * @F * POWER(@tf, @n)   
        -- r\' value   
        SET @RZ = POWER(POWER((@x - @fx), 2) + POWER((@rf - (@y - @fy)), 2), 0.5)   
        -- t\' value   
        SET @tz = POWER((@rz / (@smjrF * @F)), (1 / @n))   
        -- thetha\'' value   
        SET @zz = ATAN((@x - @fx) / (@rf - (@y - @fy)))   
        -- latitude trial value in radians   
        SET @latTR = (@pi / 2) - (2 * ATAN(@tz))   
        -- latitude iteration 1 value in radians   
        SET @lat1R = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@latTR))) / (1 + (@e * SIN(@latTR))), (@e / 2)))))   
        -- latitude iteration 2 value in radians   
        SET @lat2R = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@lat1R))) / (1 + (@e * SIN(@lat1R))), (@e / 2)))))   
        -- latitude iteration 3 value in radians   
        SET @lat3R = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@lat2R))) / (1 + (@e * SIN(@lat2R))), (@e / 2)))))   
        -- latitude iteration 4 value in radians   
        SET @lat4R = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@lat3R))) / (1 + (@e * SIN(@lat3R))), (@e / 2)))))   
        -- latitude final iteration value in radians   
        SET @latFR = (@pi / 2) - (2 * ATAN((@tz * POWER((1 - (@e * SIN(@lat4R))) / (1 + (@e * SIN(@lat4R))), (@e / 2)))))   
        -- latitude trial value in degrees   
        SET @latTD = (@latTR * 180) / @pi   
        -- latitude iteration 1 value in degrees   
        SET @lat1D = (@lat1R * 180) / @pi   
        -- latitude iteration 2 value in degrees   
        SET @lat2D = (@lat2R * 180) / @pi   
        -- latitude iteration 3 value in degrees   
        SET @lat3D = (@lat3R * 180) / @pi
        -- latitude iteration 4 value in degrees
        SET @lat4D = (@lat4R * 180) / @pi
        -- latitude final iteration value in degrees
        SET @latFD = (@latFR * 180) / @pi
        -- Return the latitude in degrees     
        RETURN @latFD;
    END

 

0 Kudos
PhilLarkin1
by
Frequent Contributor
‎01-20-2022 02:23 PM

This is awesome. Thank you

0 Kudos
TN
by
New Contributor
‎04-23-2024 10:53 AM

It might be worth noting that the above code uses 39.37 / 12 = 3.2808333 for the meters to feet conversions. This is correct for the US Survey Foot, which (since 1959) is slightly different from an international foot. The difference would amount to about 1 foot per 100 miles. I presume the Survey Foot is correct for this application.

0 Kudos
WillDeLany
by
New Contributor
‎03-19-2021 08:42 AM

Hi @mpboyle ,

If you could provide those calculations (if you still have access to them), it would be much appreciated!

0 Kudos
mpboyle
by
Frequent Contributor
‎03-19-2021 09:08 AM

Fairly certain it was this publication I used for the formulas.

0 Kudos