- Home
- :
- All Communities
- :
- Products
- :
- ArcGIS Pro
- :
- ArcGIS Pro Blog
- :
- Predicting travel times with artificial neural net...
Predicting travel times with artificial neural network and historical routes
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
Guest Post by Dmitry Kudinov, Esri
Calculating travel times is a foundational piece in transportation logistics, urban design, asset management, retail, etc. At Esri, we just completed a research project where we used artificial intelligence (AI) and machine learning to train an artificial neural network to predict travel times for transportation networks with a large number of complex, hard-to-model, and hidden variables. For this project, we partnered with NVIDIA, who provided us with GP100 and GV100 cards, which made this experiment feasible form the computation standpoint.
In this blog post, we will briefly discuss the details of this project, including the neural network architecture, training data format, efficient ways to evaluate training quality, and overall results which allow for a flexibility modelling intricate transportation aspects, and a significant throughput of the trained network.
Introduction
Building a route from A to B these days is trivial: numerous services and applications can do this for you quickly and for free. But what if you need to build a route that’s a little more complex? One which starts at your home, then goes to 3 different friends in various parts of town, then to a local produce store where you need to pick up an order you placed yesterday? But wait, the grocery store expects you at about 5pm and gets closed at 5:30pm, and it is actually located near one of the friends along the way whom you initially planned to visit first in the morning… and there is also that pesky road traffic which always gets in the way and ruins the plans.
Things become suddenly quite trickier when you want to find the best visiting sequence which also has expected arrival times.
Challenge 1: Computational complexity
Logistics companies work with even more challenging requirements, scheduling not just multiple stops, but for multiple vehicles simultaneously. Large companies, while doing next day planning, schedule thousands of stops with hundreds of vehicles per day as a single optimization problem. Now you can start getting a sense of the computational complexity and resources involved in such operations.
Challenge 2: Model complexity
Another challenging area is hard-to-model aspects of transportation:
- Changes in road speeds caused by seasonality and periodic weather patterns,
- User preferred routes,
- Individual driving habits and/or vehicle features affecting performance,
- Individual commute preferences (especially important in urban areas and multimodal transportation, e.g. predict how long will it take a person to get to a chosen store to pick up her online-placed order), etc.
Although some of these aspects are even hard to formalize and even harder to represent with traditional algorithms, these are the integral properties of modern transportation and are already captured but buried deep inside individual GPS tracks.
The experiment
While the former large-scale logistics challenge asks for high throughput computations, the latter scenarios demand greater degree of flexibility without increasing complexity of the model.
Here at Esri, we decided to see if both requirements can be met with the help of machine learning. We used a simulated set of 300 million “journeys” (GPS tracks represented only by two locations - departure and destination, departure time, and how many minutes it took to travel, Figure 1) covering the region of California and Nevada roads to train an artificial neural network to predict travel times on the transportation graph.
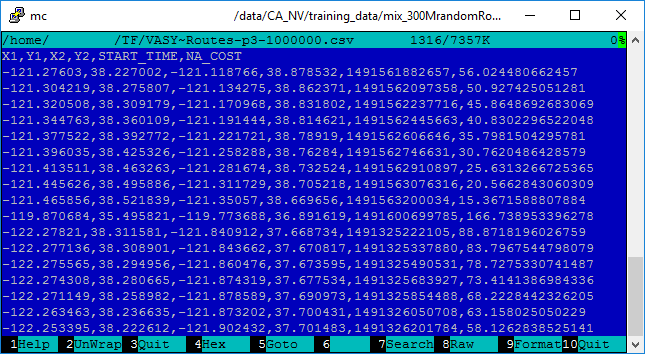
Figure 1. "Journeys" used to train the neural network. X1, Y1 – coordinates of the departure location; X2, Y2 – destination location; START_TIME – departure time in UTC milliseconds since Jan 1st, 1970; NA_COST – time it took to travel in minutes.
Despite the simplicity of the input data, the neural network, after being trained, was able accurately predict travel times between any two locations in California and Nevada taking departure time into account, effectively embedding the road congestion factor into its function.
Once trained, the neural network can produce predictions with enormous throughput: a single desktop machine with a NVIDIA GV100 card can calculate over 300,000 ETAs per second, which is two-to-three orders of magnitude faster than common traditional deterministic algorithms. Of course, a prediction produced by a neural network is an approximation, but with a controllable accuracy - we will talk more about it below. For now, it is important to mention, that such a throughout may address the first challenge: logistics companies use various algorithms to solve multivehicle scheduling problems, and at the core of most of them lies the so-called Origin-Destination Cost matrix which needs to be calculated first, filled with ETAs for any possible combination of two stops, i.e. if we need to visit 1,000 stops, the OD Cost Matrix will have 1,000,000 ETAs. Our neural network can completely populate this matrix in only three seconds!
The second challenge, flexibility, has a promising future too: while being trained with just simple two-point GPS tracks, the neural network successfully figured out accurate representation of road congestion patterns, which makes it flexible enough for further finetuning with user preferred routes, or adapt to individual driving habits, or commuter preferences.
The details
For this experiment we partnered up with NVIDIA team, who provided us with multiple GP100 and GV100 cards. The strong GPUs gave us the ability to train neural networks of realistic size and the various experiment times were shortened by twenty to fifty-plus times (thanks to massive parallelization of matrix operations needed for training). This made the search for optimal neural network architecture and numerous hyperparameter values feasible and effective. A simple example: we spent about eight months of running one of the GP100 cards 24-7 in a search for an efficient architecture, spatial and statistical distributions of the training set, good values for multiple hyperparameters. The machine had 4 (8 hyperthreaded) Xeon(R) CPU E5-1620 v2 @ 3.70GHz CPU cores. After we compared single epoch training time between the GP100 and of the same machine CPU – the difference was over fifty times! This translates the above eight months of GPU time into over 30 years of CPU!
OK, let’s get back to the details. We used TensorFlow + Keras libraries to build a dense fully connected neural network (multilayer perceptron (MLP)) with sixteen hidden layers and ten million trainable parameters total. To reduce the overfitting, we added a Dropout node right before the output layer. The input was represented by normalized pairs of coordinates for departure and destination locations, and departure time; the output – single value showing the number of minutes it took to travel from A to B at given time.
We used Mean Squared Error (MSE) as the loss function, and Adamax optimizer with initial learning rate of 1e-3.
Training was performed for 4,000 epochs total on consecutive subsets of 20 million journeys, simulating “online” training. By the end of training, the MSE value on validation set was at about ~13.5.
But how good is MSE of ~13.5? Can the neural network be usable at this point? Well, MSE of 13.5 translates into 3.7 minutes of standard deviation of predicted values being off from the ground truth… but the routes in California-Nevada region may differ significantly in size: 3.7 minutes difference may be OK for an hour-long route, but for a route which is under 10 minutes - that’s a big difference. So, a chart showing how prediction accuracy varies depending on route length can tell a better story – Figure 2.
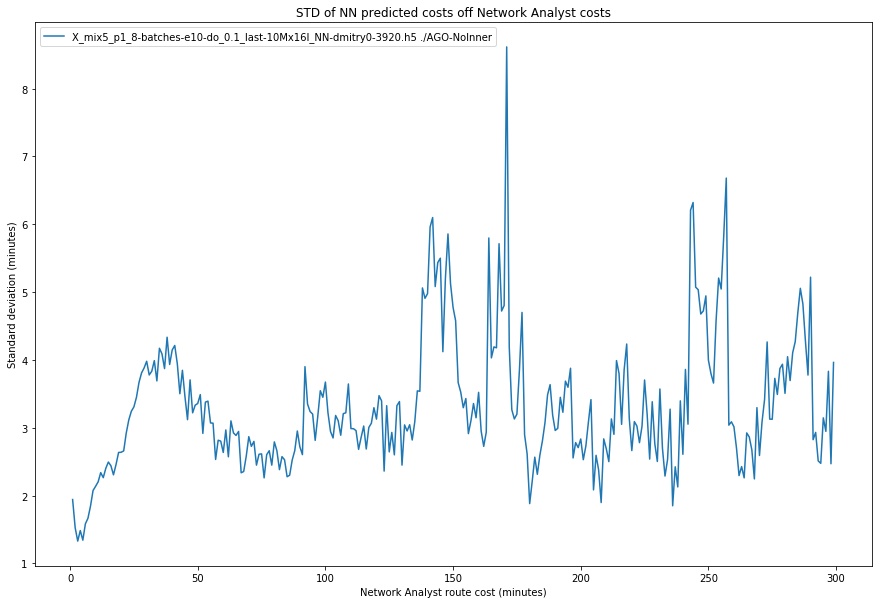
Figure 2. Variation of prediction accuracy as a function of route length.
Another great tool for evaluating prediction accuracy which we built here in Esri, is a WMS REST service endpoint wrapping our trained neural network. The service returns a geographically bound PNG containing travel time surface, where every pixel is colored proportionally to the time it takes to reach it from the central pixel. Once constrained by a maximum travel time value, such surface looks like a isochron polygon. Figure 3 shows isochrones being built around San Francisco:
Figure 3. Isochron polygon constrained by 20-minute travel time.
If such isochrones remind you of Network Analyst Service Area polygons, you are not mistaken: ultimately, in such form, both represent “reachability” zones and, if our neural network was trained well, these two should match closely. Figure 4 shows how neural network produced isochron (blue) matches Service Area polygon (red) built for the same departure location and time of day. Note how closely the boundaries of two polygons match in places where they both intersect with the streets. It is also important to note, that San Francisco area is particularly challenging due to an intricate coastal line and uneven distribution of transportation graph elements, and nevertheless, our neural network gets a good grasp on this complexity producing very compelling predictions.
Figure 4. Neural network isochrons (blue) and matching Service Area polygons (red).
So, what about the road congestions which we mentioned before? Here is the last animation for today, Figure 5, showing how a 25-minute isochron changes over a 24 hours period. You can see how the isochron shrinks during the business hours, and how it expands back during the night.
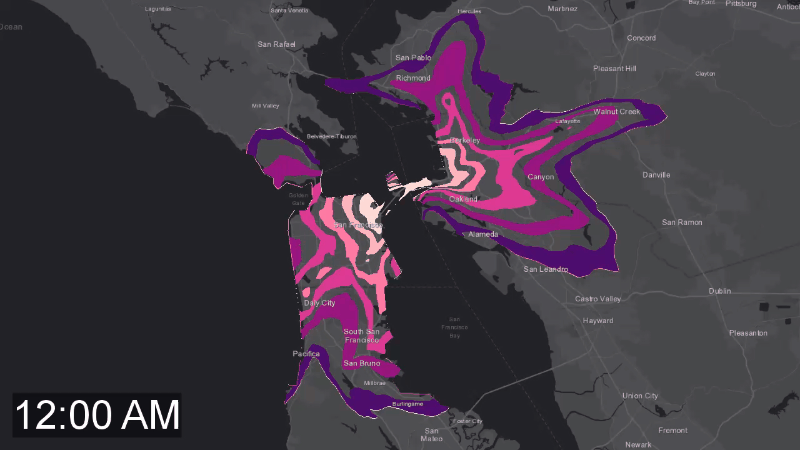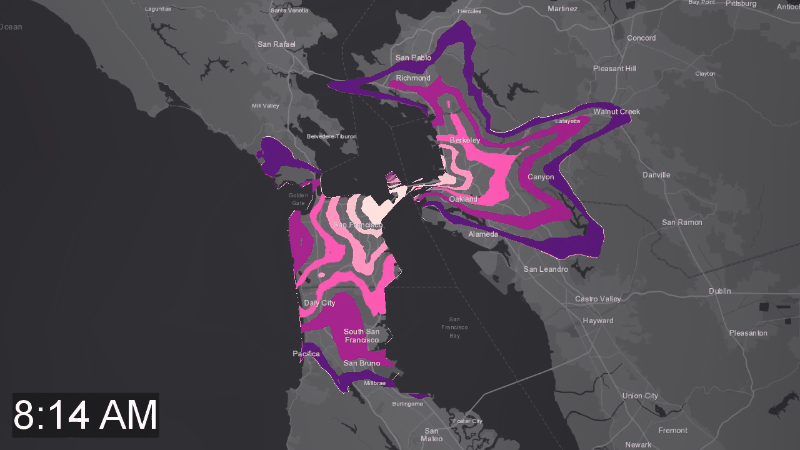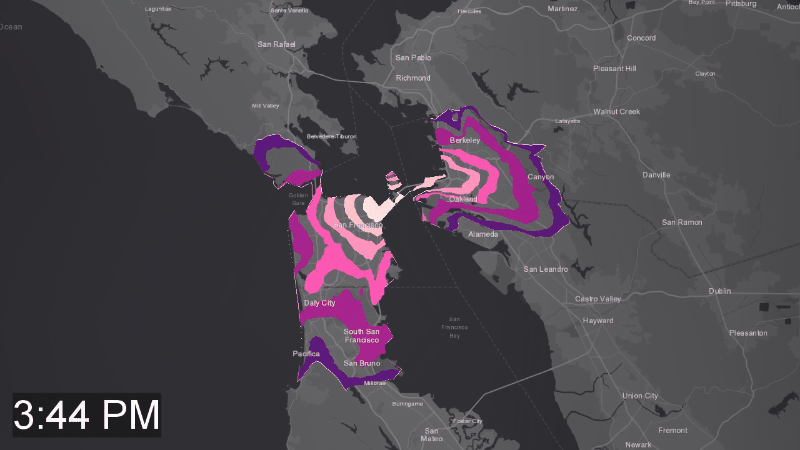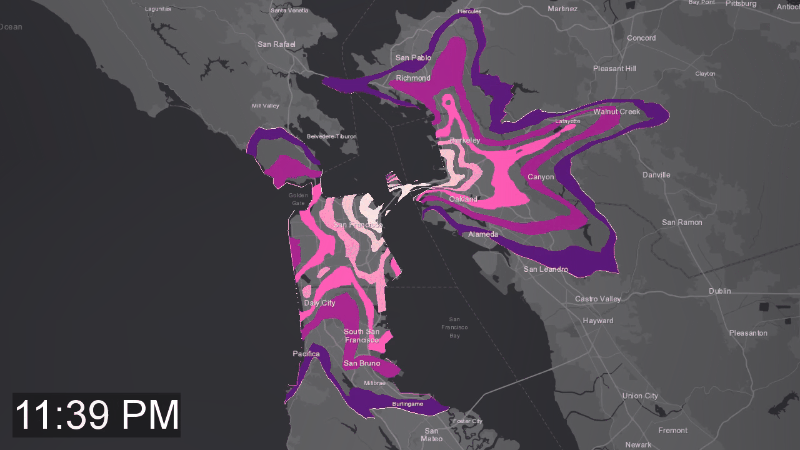
Figure 5. Road congestion patterns captured by the neural network during training. There corlor rings were added for visualization purposes and are similar to isolines of a continuous 3d surface, where the 3rd dimension is time. That animation has 12 rings colored (or left transparent) for ranges of travel times falling into 125 second buckets – 12 total, summing up to 25 minutes.
The road ahead
Although we have achieved here some impressive results, there is room for improvement. One particular path which we want to explore further down the road, is to check the applicability of one-dimensional convolutional network instead of MLP. The reason for this is simple: there is a strong correlation between the coordinates, and multiple repeating patterns in the training data – this makes our scenario a good candidate for a convolutional architecture which will scale better for larger geographical areas.
Another area of improvement can be illustrated with the Figure 2 above: we want smaller standard deviation values for shorter routes, and this can be achieved by more accurate selection of the training data, giving shorter routes a bigger share in the training set.
And, of course, the final step – using the trained neural network in transportation analysis and planning.
We will keep you updated on the progress.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.