- Home
- :
- All Communities
- :
- Products
- :
- ArcGIS Pro
- :
- ArcGIS Pro Questions
- :
- Create mean center (point-feauture) out of multipl...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Create mean center (point-feauture) out of multiple points within a polygon
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
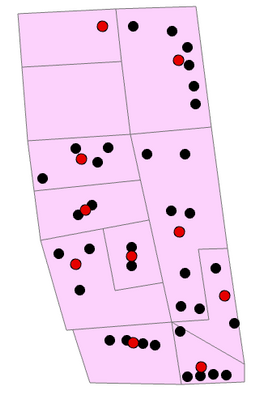
Hello, I´m using ArcGis Pro for a study project.
I have two feature classes. One polygon feature and one point feature. The points lay within the polygon features. (see attached image)
Is it possible to create the mean center of the points who are within one polygon? (like the red dots on the image)
I know I can do every polygon by its own but i have a really big dataset, so this is not an option.
Thanks for your help:)
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Intersect the point and polygon fcs
- Dissolve the resulting point fc by the polygon id field into a multipoint fc
- run Feature To Point on that multipoint fc to get the centroids
Have a great day!
Johannes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I wonder if the Mean Center (Spatial Statistics) GP tool would work as long as the points feature class had a case field (i.e. number/text) for those points that fall in one polygon. For example, 10 points fall in polygon with a case field of 1001. Then you would have a mean center of those points in polygon 1001, 1002, etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Intersect the point and polygon fcs
- Dissolve the resulting point fc by the polygon id field into a multipoint fc
- run Feature To Point on that multipoint fc to get the centroids
Have a great day!
Johannes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Be aware that this approach does not guarantee that the centroid is in the polygon!
Have a great day!
Johannes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I wonder if the Mean Center (Spatial Statistics) GP tool would work as long as the points feature class had a case field (i.e. number/text) for those points that fall in one polygon. For example, 10 points fall in polygon with a case field of 1001. Then you would have a mean center of those points in polygon 1001, 1002, etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Right, running Mean Center on the Intersection of the points and polygons (for the case field) gives the same result as Dissolving and converting to centroid.
Have a great day!
Johannes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Of course one could determine the polygon centroids/label points, which may be as appropriate as the point centroids and it would ensure point-in-polygon tool.
If distance to some measure of centrality is needed, be sure it is the centrality of the points that is critical and not their dispersion within the bounding polygon. In which case a centroid of the convex hull of each point cluster may be more appropriate or as appropriate
... sort of retired...