- Home
- :
- All Communities
- :
- Products
- :
- ArcGIS Network Analyst
- :
- ArcGIS Network Analyst Questions
- :
- Two Facilities for Each Demand
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Two Facilities for Each Demand
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
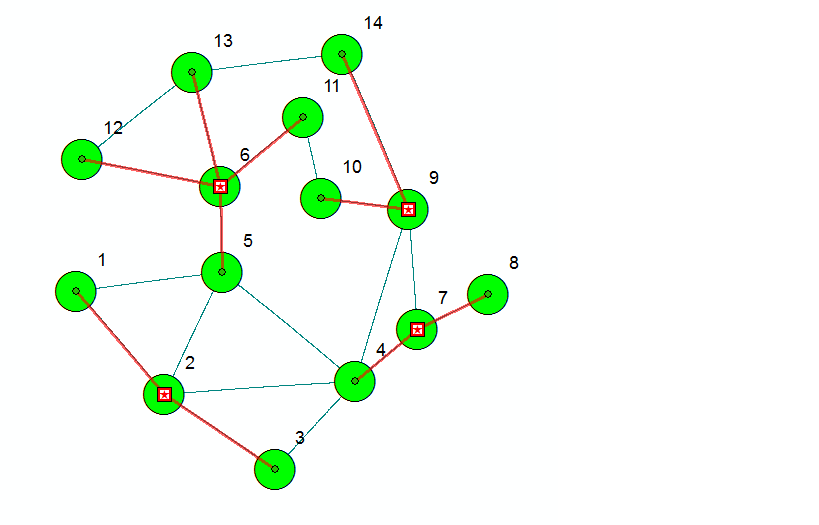
I was reading the Network Analyst Help to see if possible how to assign at least two facilities (Red in the figure; result of analysis) for each demand (Green; data I have) using location allocation tool. I want to find those locations for the facilities so that all demands can reach at least two facilities through only one road. The figure is for the case when one demand can reach at least one facility.The graph is just for example.
Any idea?
Thanks in advance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Something that I haven't looked at, but you can use required and competitor facilities to the analysis... the details are somewhere else in the documentation but the general discussion may be of interest to you
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Thanks Dan. Probably, there's no "direct" solution provided by the network analyst toolbox as for the case of a facility per a demand (minimize the facilitirs). It's the same problem but for the case of contingency or outage n-1 of facilities. That is, solve the problem and find the number of facilities with their locations to minimize the total number of facilities so that every demand has a connection to at least two facilities; just in case one of them is in outage or maintenace but the other one should be in service.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
You can come up with a couple of solutions:
1. Once you have solved Location-Allocation once, you can set up a Closest Facility solver, load the chosen LA facilities as CF facilities, demand from LA as incidents in CF and solve for 2 closest.
2. You can solve Location-Allocation for the "first" facility. Then remove the chosen one and solve again. Now you will have the second facility. You will probably have to do this once for each chosen facility in your original solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
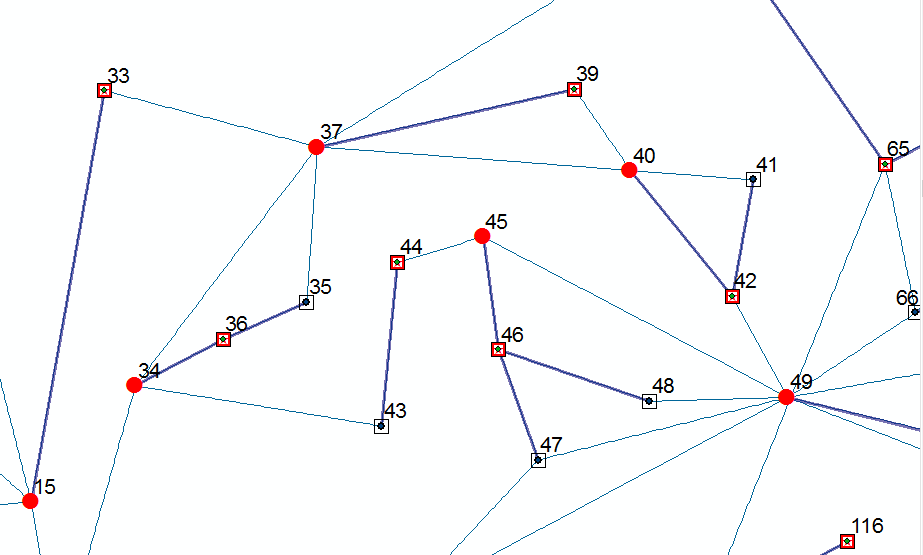
Thanks Jay; that is a brilliant idea I haven't thought about. But still the result shows some extra facilities since we deal with the problem as two different problems and two separate objective functions. For instance, node-33 and node- 39 in the figure below (I applied your steps of method-2) are not necessary to have them for minimization of facilities. Node-33, with having a facility at its location, still can reach a facility, say node-15, while the other one, node-37, in out of service and vice versa. The same thing is true for node-39. You may ask what about the rest neighbor nodes, for example, node-40, if there is no facility at node-39? still node-40 can reach at least one if the other one is lost.
I've tried your first method as well but for some reason I did not get any reasonable result; I got a facility at each node of my of network.
Thanks Jay and Dan for your ideas.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Sorry I do not understand what you are saying about what is shown in the figure you attached.
Jay
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Thanks Jay and sorry I was not clear in my last comment.
I've applied your idea (method 2) on a network with 118 nodes and the last graph was a part of it. I followed your two steps. The red circle points are from step 1 and the red square points are from step 2.
Now, there are some facilities (the two red points) I can delete them while still I have for every node of the whole network at least two facilities.
For instance, delete node-39 and you will still have at least 2 facilities connected for each node;
Point 40 has 3 facilities connected to (40, 42 & 37),
Point 37 has 2 facilities (37, 40 & 34)
So, the final solution from the two steps is not a minimum optimal solution for locations of facilities because we can delete some of these facilities and get the objective of the problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Does that make sense? That is true for the node-33 as well. I found out that these extra facilities are located on points with two lines connected to. Any idea to find those points and delete them? I have a network with more than 2000 nodes which is not easy to find all of these additional facilities.