Spearman's rank or Pearson's correlation coefficient?
Yes as you describe. It may be useful to use existing classifications if they are available in the census categories, or you could use means and std devs to produce your classes or just subdivide the % data based upon some criteria of your choosing.
for example
high > =1 std dev
norm -1 std - 1 std dev
low < = -1 std
as an example should the distribution appear normal, this will give you some supportable criteria. Should the %age data not be normal, then you might want to examine the distribution to assess break points.
The key point is .... your categories, when derived from interval/ratio data, need to have some kind of justification! you could get the "how did you produce those classes" or "why did you choose those classes" questions (we examiners are not a cruel lot...just looking for thoughtful consideration and not a "because?!" person)
in any event, plot you data first to see if there is any clustering/pattern/ etc in the data, then do your descriptive statistics...then and only then, choose your inferential test. Parametric statistics has its requirements and if the data don't conform, then your non-parametric options (eg. chi) can step in.
Good luck and post more questions and/or graphs if needed.
PS I hope your advisor and committee are giving you similar advise.... take theirs over mine should there be a disagreement. If none is forthcoming, pose these issues with them...there are individuals that really don't care about appropriateness of the test and would say use pearson's but do it versus transformed data... eg log(%) versus sqrt(distance)+0.137 ... just so the distribution becomes 'normal'-ish 
but that is another isssue
Ok then, thank you
My supervisor seemed to think that using either pearson's or spearman's would be ok, but wasn't sure which would be more appropriate.
Can I just clarify that both my variables are ratio variables? If they are then I'm assuming that spearman's probably wouldn't be as appropriate to use as pearson's since spearman's is better used for ordinal variables? But I understand that variables have to vary linearly in order for pearson's to be carried out and I'm uncertain whether this is the case or not for mine? Here are the scatter diagrams I've plotted for them at the moment. I'm also measuring access for older individuals and those considered disabled, as well as for children.
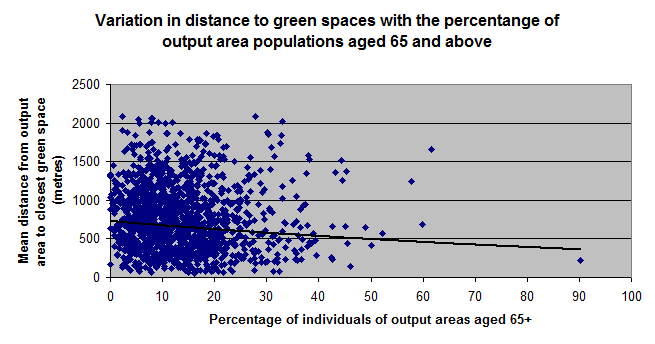
Or if I transformed the data so that it becomes normal, as you describe, would it solve the data not being linearly related being an issue? I'm not too sure how to go about doing this though. Thank you.
Yes, I've actually already made some maps Here are the ones I've created to assess variations in access for the older individuals of the population, to identify areas which priority should perhaps be given to in improving accessibility. The first shows the percentages of the population of each output area who are aged 65 and above, as well as the distribution of green spaces. And the second shows the average distances to the closest green space for each output area.
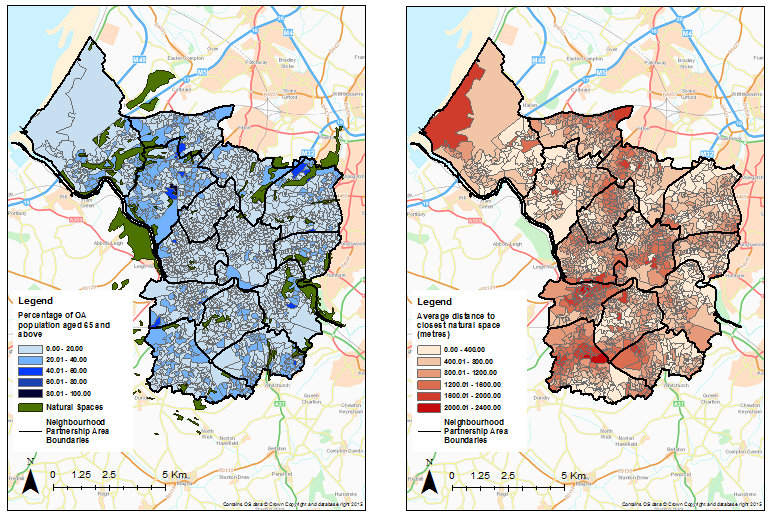
It's a bit hard to compare them both though because of how many output areas there are and how small they are. But I suppose it can just about be seen that the average distance to the closest green space is fairly low for the only area with over 80% of the population over 65, being less than 400 metres. Then most of the areas in which 40-60% of the population are over 65 have slightly higher average distances of between 400-1200 metres. But most areas with poor access, over say 1800m, seem to have smaller older populations. So perhaps it could be said that, in this case, the distribution of the spaces seem to be reasonably fair in the sense that areas where access is poorer, above say 1200m, tend to have smaller populations of older people, if it's assumed that good access should be prioritised for older people. But I can use arcmap to analyse this a bit more carefully though by looking at the attribute tables for each variable.
I should probably change the classification colours for the second map so that it's a bit easier to distinguish between the categories for the output areas as well. And perhaps it would be good to combine both maps into one, but I can imagine this would be quite difficult to interpret and not very clear.
