- Home
- :
- All Communities
- :
- Products
- :
- ArcGIS CityEngine
- :
- ArcGIS CityEngine Questions
- :
- Split Shapes with different way?
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
How to split blocks into equal lots randomly.Block parameters do this, but they are minimum and maximum space based. I want to be able to do number based identification.For example recursive-offset or skeleton subdivision splitting 3,5,10(how many pieces do I want) pieces. Is it possible?
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Okay I understand. You just need to work through the logic and the math. First split off the first parcel in one direction - I think z if we align our scope. Then divide up the rest by the even number with a split on the x-axis. If we are only doing 3 subdivisions then its easy, just divide in half. But if we are doing more than 3 we split in half and then split again for what is remaining (our EvenSplit). Hopefully you can follow the logic.
@Range(3,5,7,9,11)
attr NumSplits = 3
@Hidden
attr EvenSplits = NumSplits - 1
Shape-->
alignScopeToGeometry(yUp,1)
SplitShapes
SplitShapes-->
case NumSplits == 3:
splitArea(z) {geometry.area/NumSplits:NewShape | ~1: split(x){'0.5:NewShape | '0.5:NewShape}}
else:
splitArea(z) {geometry.area/NumSplits:NewShape | ~1: split(x){'0.5:splitArea(z){~geometry.area/EvenSplits*2:NewShape}* | '0.5:splitArea(z){~geometry.area/EvenSplits*2:NewShape}*}}
NewShape-->
print(geometry.area)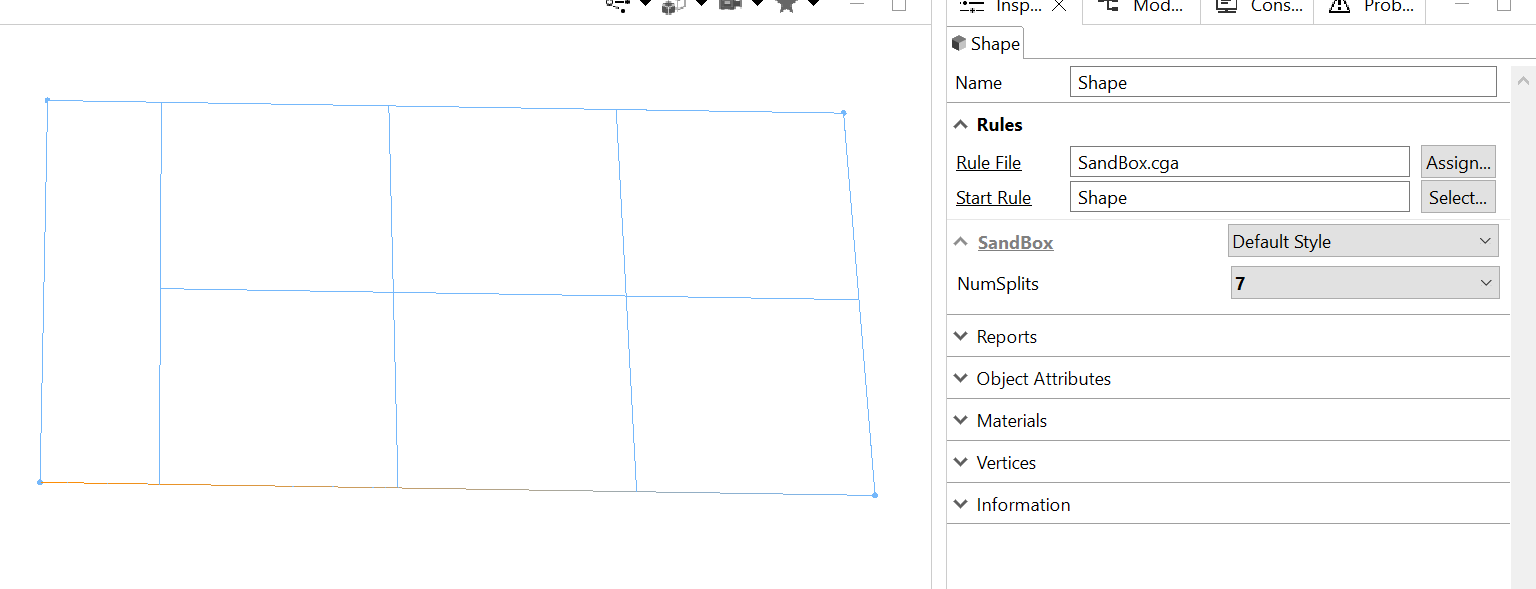 and the console reports the areas to be just about exact
and the console reports the areas to be just about exact
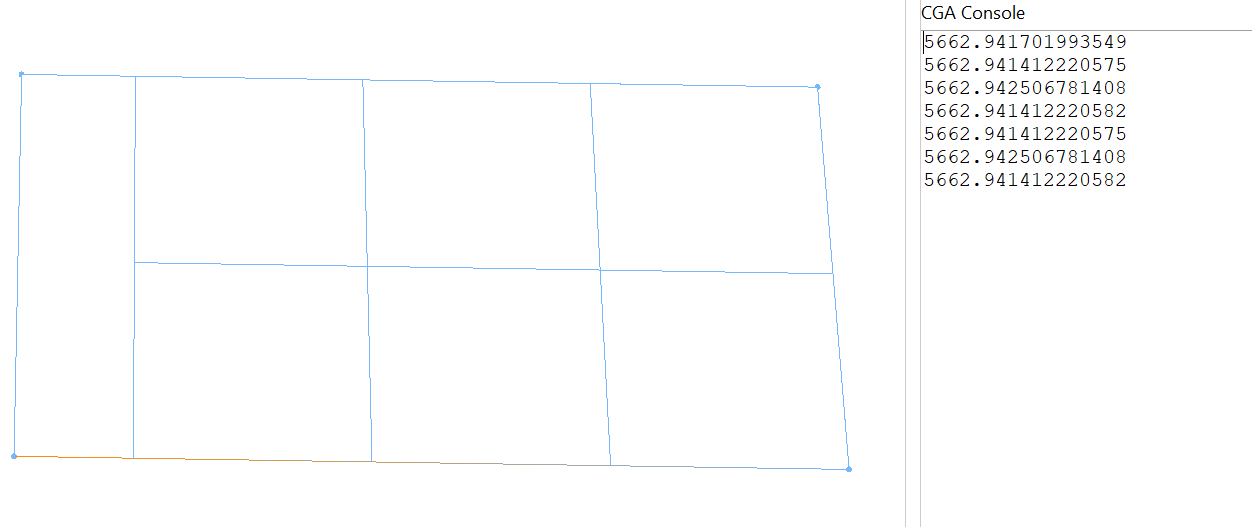
Look good?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Do you mean control the number of splits of shape? Something like this would do it.
@Range(0,100)
attr NumSplits = 3
Shape-->
split(x) {scope.sx/NumSplits:NewShape}*You can also split by area. This code makes sure every subshape is the same size.
@Range(0,100)
attr NumSplits = 3
Shape-->
splitArea(x) {geometry.area/NumSplits:NewShape}*Make sense?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi Devin. The split area and the geometry area function are answering my question to a certain extent. But I want equal areas and cuttings in different axes same time.Like my example.How can I do that? btw,thanks for reply.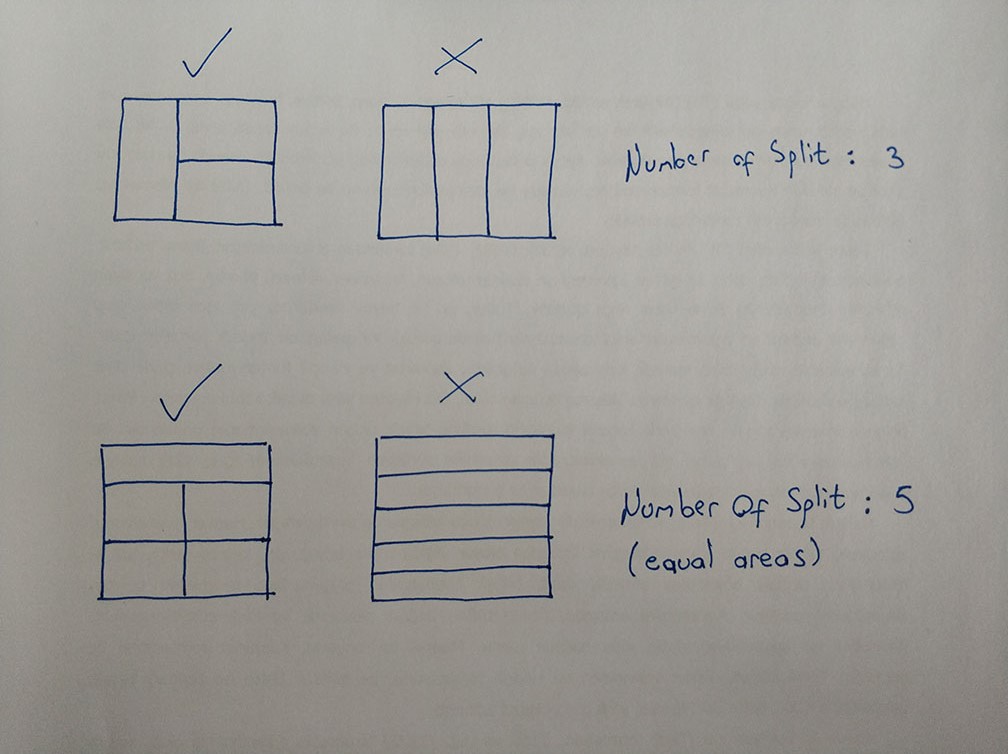
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
splitArea Operation
Lot --> SplitArea(3) SplitArea(n) --> case n == 0 : A case scope.sz > scope.sx : splitArea(z) { ~1 : SplitArea(n-1) | ~1 : SplitArea(n-1) } else : splitArea(x) { ~1 : SplitArea(n-1) | ~1 : SplitArea(n-1) } |
| The block is divided recursively three times using splitArea. Each split divides the shape perpendicular to its longest axis into two parts of equal area. Each lot is colored by its area such that lots with the same area have the same color. Using splitArea, all the lots are yellow because the block is divided into equal area lots. |
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Okay I understand. You just need to work through the logic and the math. First split off the first parcel in one direction - I think z if we align our scope. Then divide up the rest by the even number with a split on the x-axis. If we are only doing 3 subdivisions then its easy, just divide in half. But if we are doing more than 3 we split in half and then split again for what is remaining (our EvenSplit). Hopefully you can follow the logic.
@Range(3,5,7,9,11)
attr NumSplits = 3
@Hidden
attr EvenSplits = NumSplits - 1
Shape-->
alignScopeToGeometry(yUp,1)
SplitShapes
SplitShapes-->
case NumSplits == 3:
splitArea(z) {geometry.area/NumSplits:NewShape | ~1: split(x){'0.5:NewShape | '0.5:NewShape}}
else:
splitArea(z) {geometry.area/NumSplits:NewShape | ~1: split(x){'0.5:splitArea(z){~geometry.area/EvenSplits*2:NewShape}* | '0.5:splitArea(z){~geometry.area/EvenSplits*2:NewShape}*}}
NewShape-->
print(geometry.area) and the console reports the areas to be just about exact
and the console reports the areas to be just about exact

Look good?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Thats cool.Thank you for your interest Devin.