- Home
- :
- All Communities
- :
- Products
- :
- ArcGIS CityEngine
- :
- ArcGIS CityEngine Questions
- :
- Acute angle check?
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Acute angle check?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hello there,
Is there a way in CGA code to check if a 2D scope contains any acute angles? The reason I ask is that I don't want to generate a building on any lots with acute angles (generate a Park instead maybe). I can check for 3 sided lots and rule them out, but it doesn't help with cases like this . . .
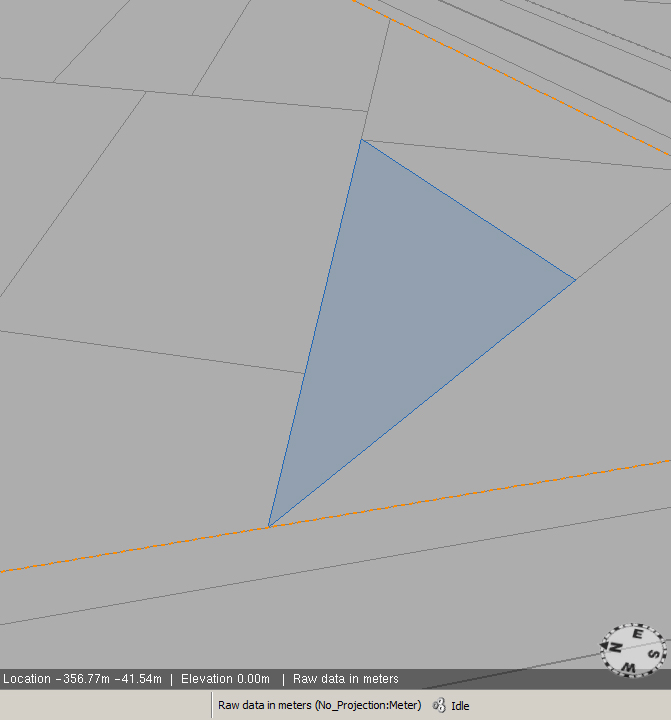
. . . .where there are 4 verts and 4 'sides' even though 2 of the sides are co-incident. Checking for an acute angle would solve this, as there are 2 acute internal angles. This strikes me as quite a basic thing to want to check for, before generating a building.
Any help appreciated.
Sean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Hi Sean,
to solve your task, please use the geometry.isRectangular (geometry Functions) function.
Synopsis
bool geometry.isRectangular(float tolerance)
Parameters
- tolerance
The tolerance in degrees for deciding if an angle is a right one or not.
Returns
true if all faces of the current shape's geometry consist of 4 vertices and contain only right angles, false otherwise. Angles in the range [90-tolerance, 90+tolerance] are considered to be "right".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
Sean and Thomas,
I don't have an answer, but I do have a theoretical question. I like questions that are hard to solve with a computer, but easy for a human eye to see. My question is, "what makes a lot un-buildable, and more suited for a park?"
I have had the same question on numerous projects. It can't just be "is an acute angle present". It would have to involve scale also. If the triangular shape you have highlighted was 200m long vs 20m, it would be able to build a small business park, vs no building at all.
Here's some lots that are adjacent to a railway, which could all take buildings, if wide enough (a function of scale, rather than angles):
Just curious about what other factors would be part of an "isLotBuildableOrPark" function... it would be good to define this, for general use in urban planning rules.
Thanks!
Chris
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
I think we would have to ask, what makes a lot suitable for building on? Is it because the area is large enough and not so skinny?
If so, we could use a combination of the following to make heuristics to define when a lot is suitable for building on:
* comparison of scope.sx and scope.sz. For example, for a long skinny lot, scope.sx/scope.sz will be either really close to zero or really large. For a square lot, this aspect ratio would be 1.
* comparison of geometry.area and scope.sx*scope.sz. For example, a triangular lot will have a smaller geometry.area/(scope.sx*scope.sz) ratio than a rectangular lot (assuming the scope is aligned to the shape).