Measuring Distance in 3D
3D
Math check
x [ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.],
y [ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
z [ 0., 1., 0., 1., 0., 1., 0., 1., 0., 1., 0.]
segment length/distance travelled [1.41, 1.41, 1.41, 1.41, 1.41, 1.41, 1.41, 1.41, 1.41, 1.41]
Conventional application
- Take a DEM
- Construct a 3D polyline (Z-enabled) representing a profile path along it
- Densify it at some increment if you want to sample more elevation points along the line, but are too lazy to do it as you go (or you forgot). This is optional, but there are builtin tools and/or 3rd party tools to do this (including some of mine)
- Feature vertices to points, to get the path as points
- Poly* features to points .... any license from Polygon_polyline_tools, or
- feature-vertices-to-points .... Advanced license
- Extract values to these points.
- Extract Values to Points in the Spatial Analyst
- If you don't have SA, there are ways to get these data, but that is for another blog
- Add Geometry Attributes to get the x, y and z values for the points.
- Off to numpy
The Map and the Profile
Start low, go high, or vice versa. Vertical exaggeration on the Z values
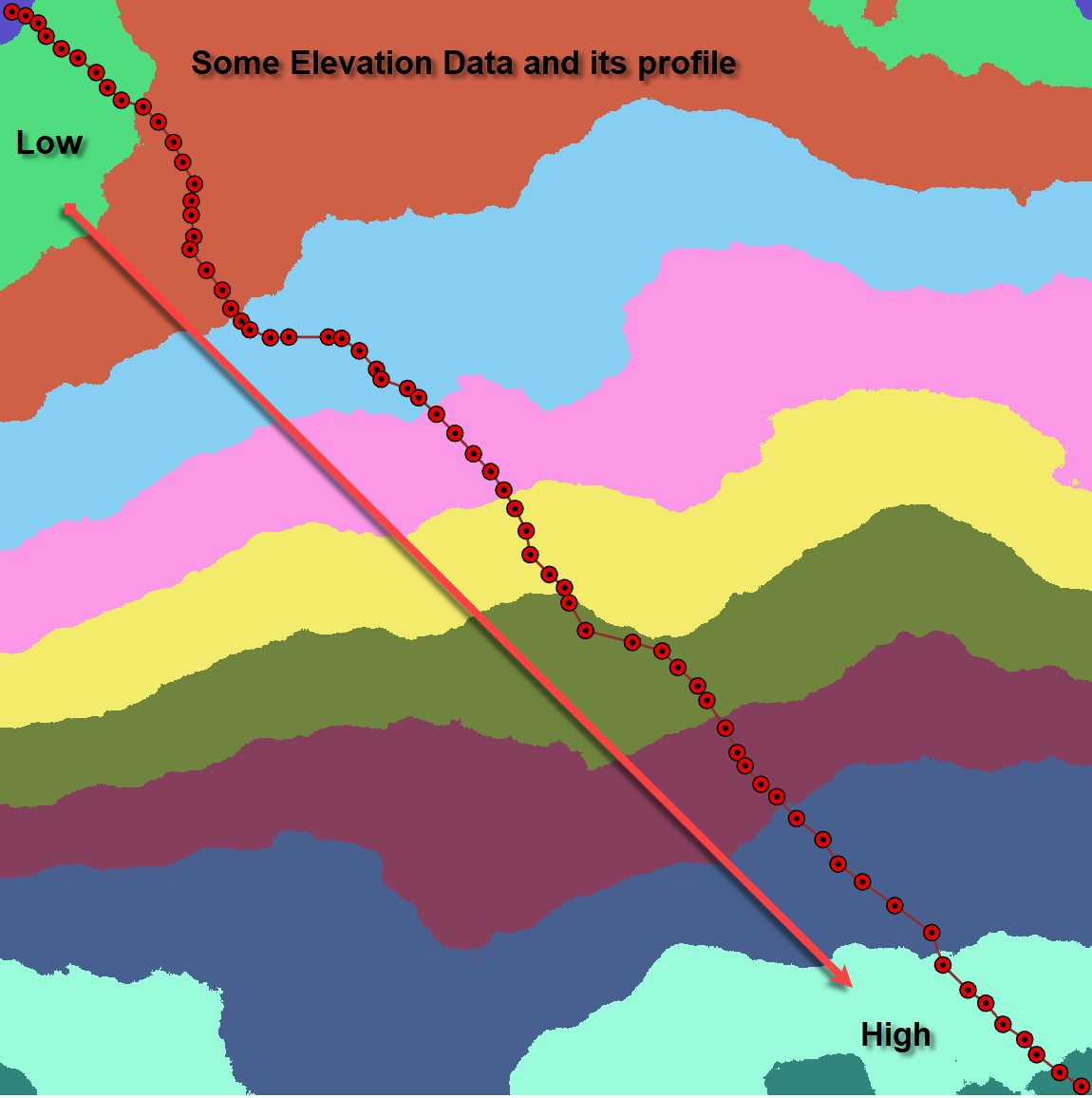
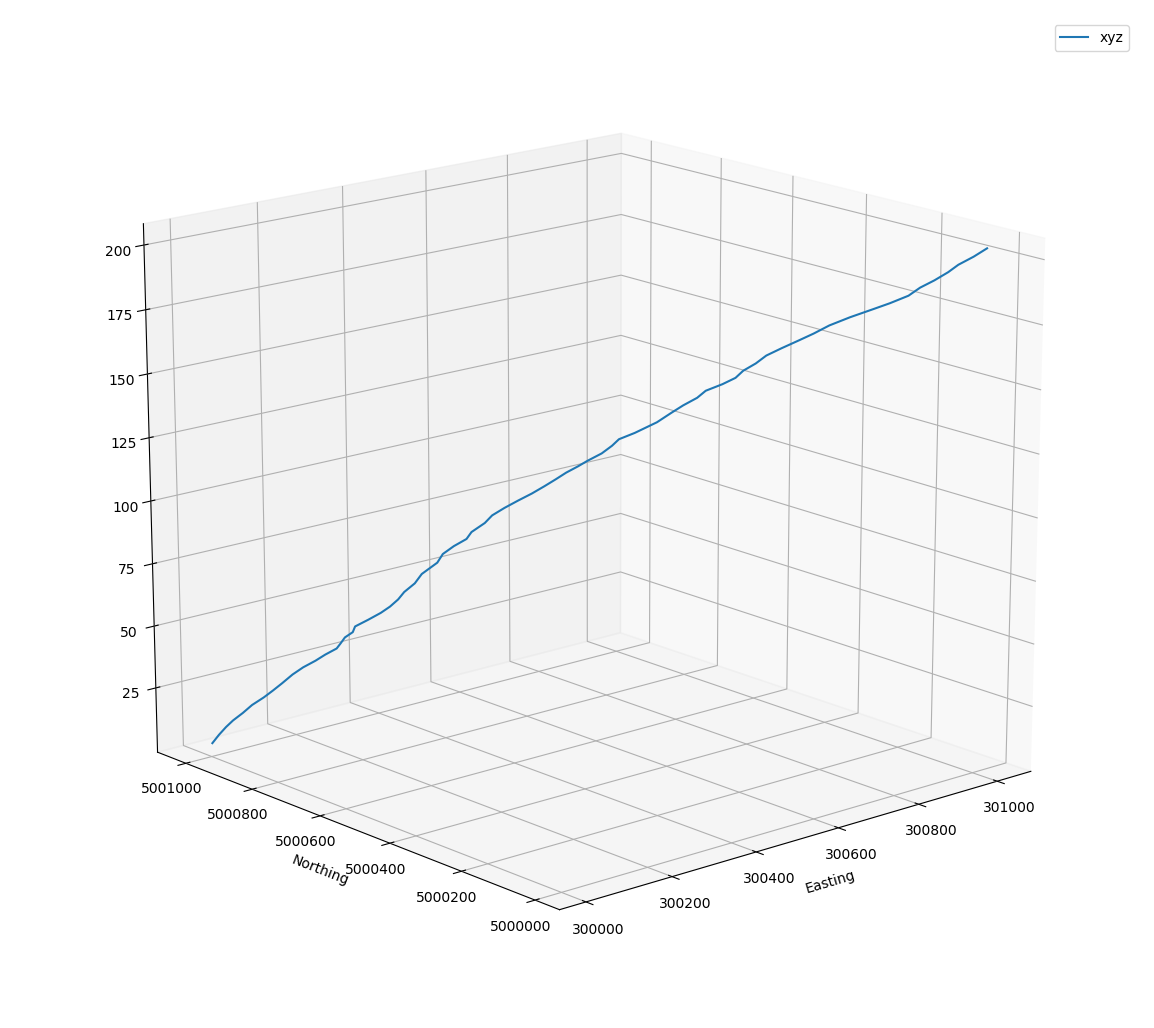
Calculations
Now for some distance calculations.
Points
array([[ 300012.56, 5001013.9 , 3. ],
[ 300025.53, 5001010.2 , 6. ],
[ 300037.26, 5001003.4 , 9. ],
...,
[ 300972.11, 5000037.68, 198. ],
[ 300993.72, 5000021.01, 201. ],
[ 301014.1 , 5000008.04, 204. ]])
2D Total length, sequential lengths
- 1505.25,
- array([13.49, 13.56, 14.4 , 18.42, 17.69, 21.99, 17.66, 17.49, 21.29, 20.08,
... snip
37.54, 42.86, 32.03, 33.18, 20.75, 25.46, 24.84, 18.03, 27.29, 24.15]))
3D Total, sequential
- 1519.95,
- array([13.82, 13.88, 14.71, 18.66, 17.94, 22.19, 17.91, 17.74, 21.5 , 20.31,
... snip
37.66, 42.96, 32.17, 33.32, 20.96, 25.64, 25.02, 18.28, 27.46, 24.34]))
Quick calculation
np.sqrt(204**2 + 1505.25**2) => 1519.01 Not to be unexpected given the line's shape.
Calculations made using ... e_leng ... from arraytools. The gist link allow people to experiment.
Unconventional application
How far did the turkey vulture travel before it landed on its food?
2D start-end point distance - 56.39
2D Total length, sequential lengths
- 1590.97
- array([0.16, 0.16, 0.17, 0.18, ..., 8.76, 8.79, 8.81, 8.84]))
3D Total, sequential
- 1658.26
- array([1.01, 1.01, 1.01, 1.02, ..., 8.82, 8.85, 8.87, 8.89]))
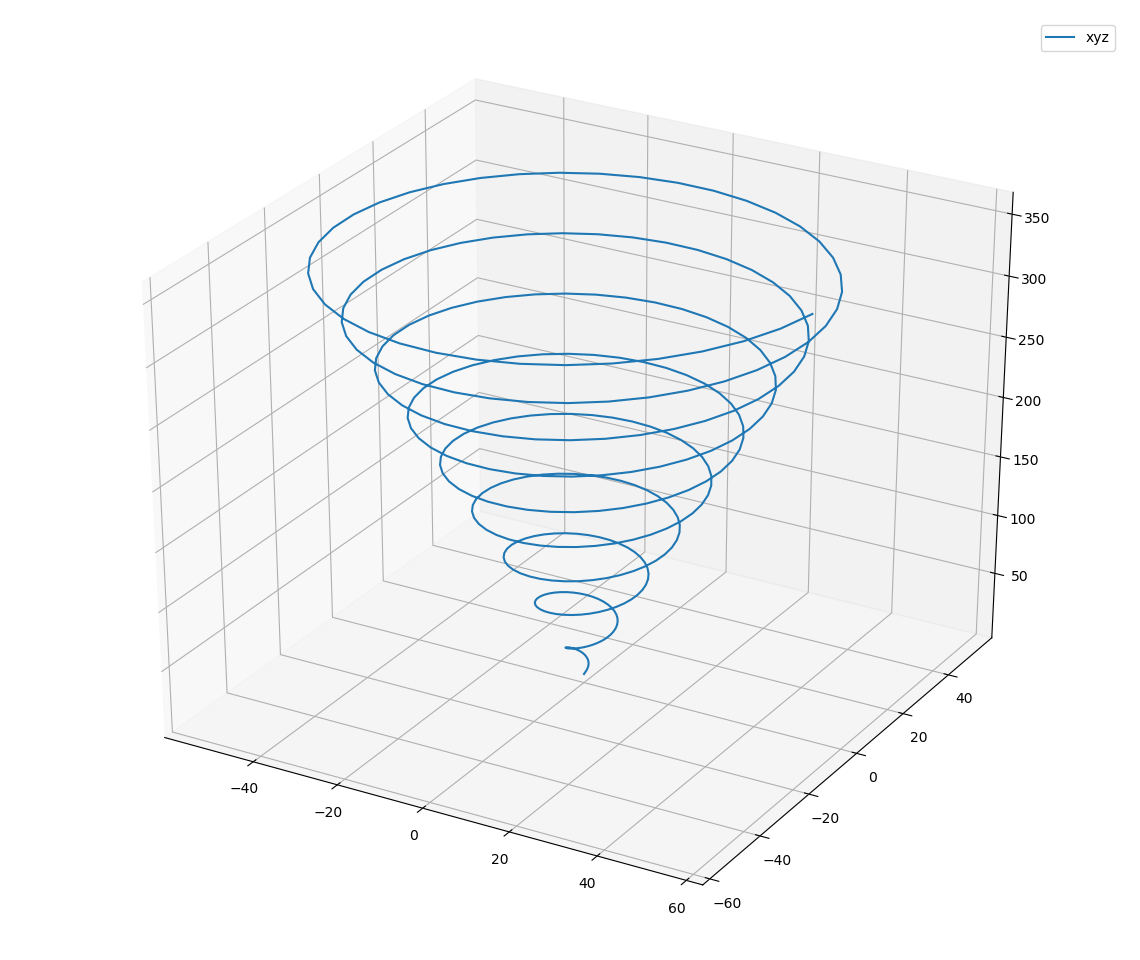Archimedes spiral in 3D 