- Home
- :
- All Communities
- :
- Developers
- :
- Python
- :
- Python Blog
- :
- Transect lines, parallel lines, offset lines
Transect lines, parallel lines, offset lines
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
Lines
Different incarnations and names
Pretty easy to form the origin-destination pairs.
Start at a point.
Throw in horizontal and/or vertical offsets.
A dash of an azimuth/bearing.
A tad of NumPy
A bit of Arcpy and....

A good way to spend some time, so you write it down because you will forget and reinvent it later.
Almost forgot...
There is always one student that thinks outside the box.
Hmmmm could be a bonus here... I wonder if any of mine can replicate the compass with 10 degree increments?
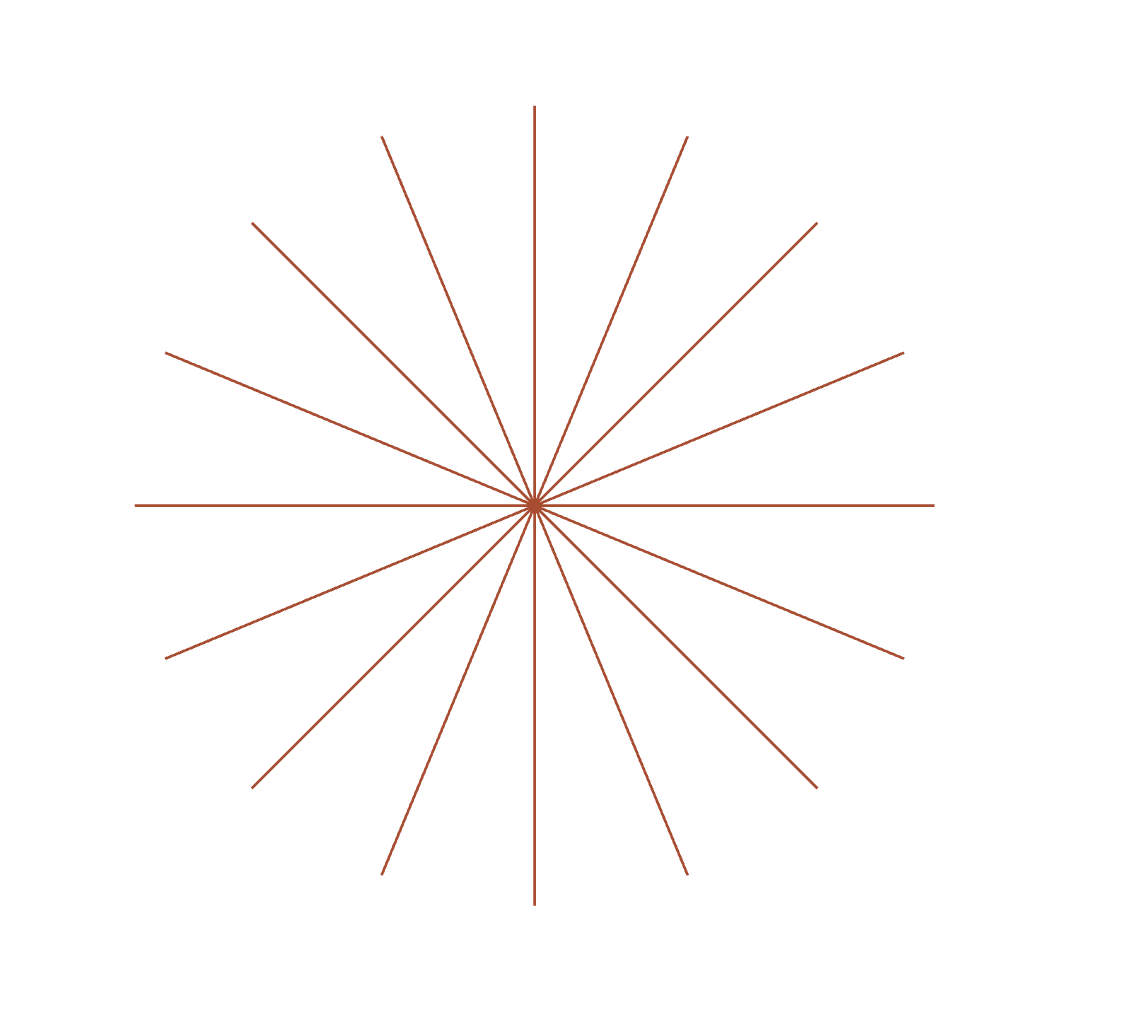
In the attached code, I made these changes
rads = np.deg2rad(bearing)
dx = np.sin(rads) * dist
dy = np.cos(rads) * dist
#
n = len(bearing)
N = [N, n][n>1] # either the number of lines or bearingsAnd used this
b = np.arange(0, 361, 22.5)
a, data =transect_lines(N=1, orig=[some x, some y],
dist=100, x_offset=0, y_offset=0,
bearing=b, as_ndarray=True)You can't have it both ways in a manner of speaking. By limiting N to number of bearings, you use numpy to generate the desired angles,. There is no x or y offset since the origin is now fixed.
How to use the attached...
""" ---- use these as your inputs, with edits of course
# ---- make the x, y coordinate table
SR = 2951 # a projected coordinate system preferably
a, data =transect_lines(N=10, orig=[299000, 5000000], dist=100,
x_offset=10, y_offset=0, bearing=-10, as_ndarray=True)
p0 = r"C:\Your_path\Your.gdb\a_tbl"
arcpy.da.NumPyArrayToTable(a, p0)
# ---- now for the lines
p1 = r"C:\Your_path\Your.gdb\some_lines"
arcpy.XYToLine_management(p0, p1,
'X_from', 'Y_from',
'X_to', 'Y_to',
spatial_reference=SR)
"""PS
The python/numpy part is quite speedy, using variants of
%timeit transect_lines(N=10, orig=[0,0], dist=1, x_offset=0, y_offset=0, bearing=0, as_ndarray=True)
10 36.0 µs ± 309 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.