Concave hulls...
Tons of examples, some suited to some point clouds, others not so much. 
It has greatly amused me over the years that people spend so much time trying to find the 'corner cases' where a particular implementation fails. For example, the ever popular C - shaped object.
I know... in optical fields, being able to identify the letters of the alphabet or curly snaked-shaped patterns is important.... but, how many times have you sent your field assistant to collect data points with weird shapes.
Toolbox links
Concave Hulls this is a separate toolbox
Point Tools or it is contained in this toolbox as well
So, regardless of the implementation, they can be illustrative in exploring point patterns and generating containers to describe them. I recently posted on the Minimum Area Bounding Ellipse (MABE) and I have a toolset that produces Minimum Area Bounding Circles (MABC), rectangles (MABR) and extent rectangles. This implementation of the concave hull was proposed by Adriano Moreira and Maribel Yasmina Santos in about 2007 and there are several implementations in various languages on GitHub for those needing a trolling session.
The 'tightness' of the concave hull by changing the number of nearest neighbors to include when you are trying to decide on which points on the perimeter to keep or dump. This 'K' factor illustrates some of the possible outcomes. The thing to watch out for is producing degenerate points which are outside the hull, but are just to much of an outsider to be allowed into the fold. So in pictoral form,
3 neighbours
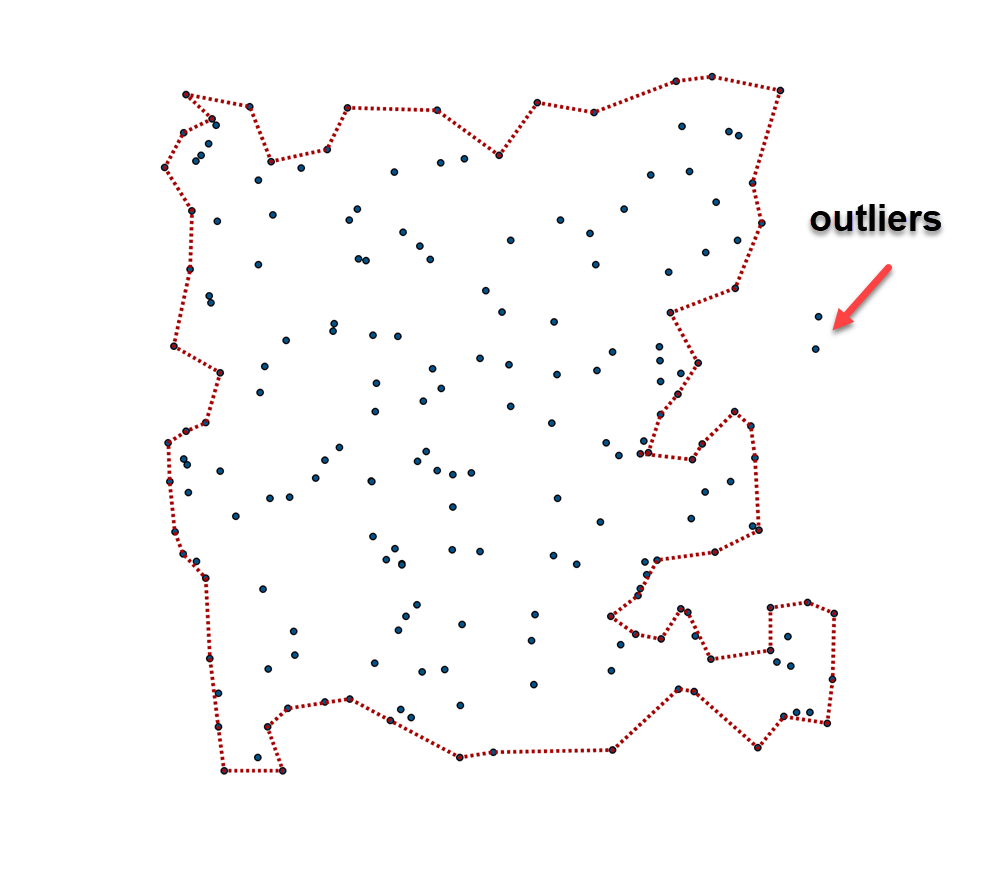
7 neighbors
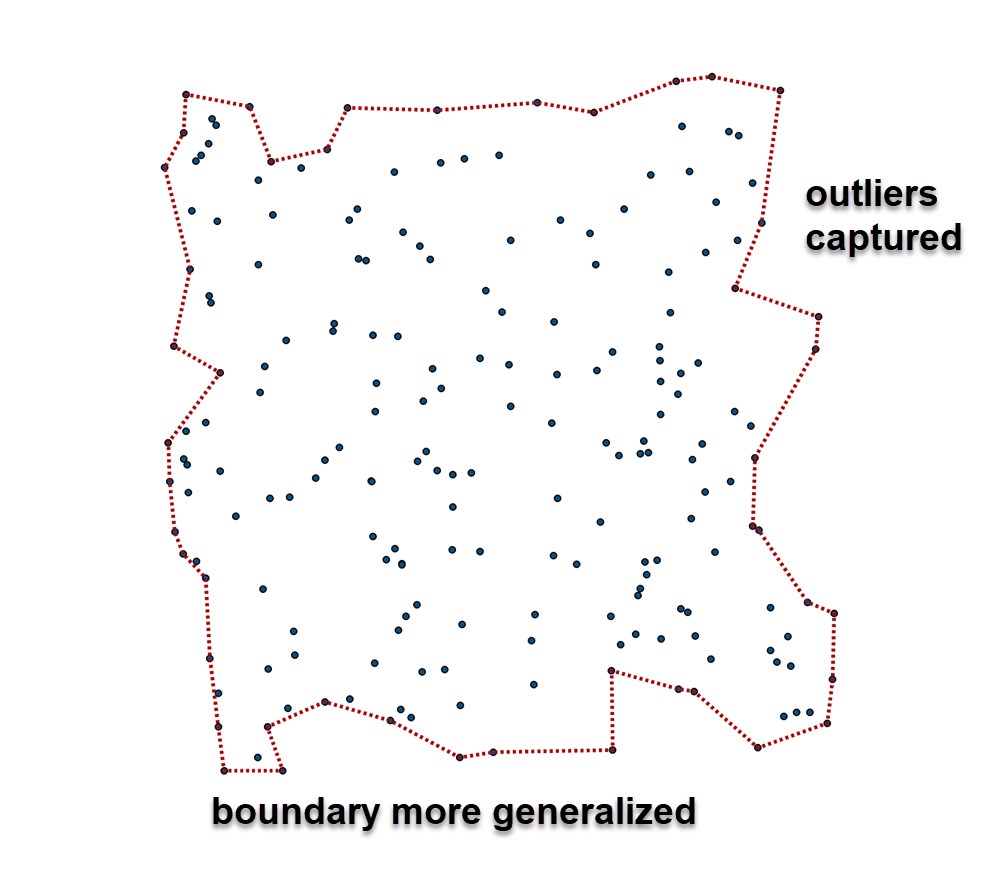
11 neighbors
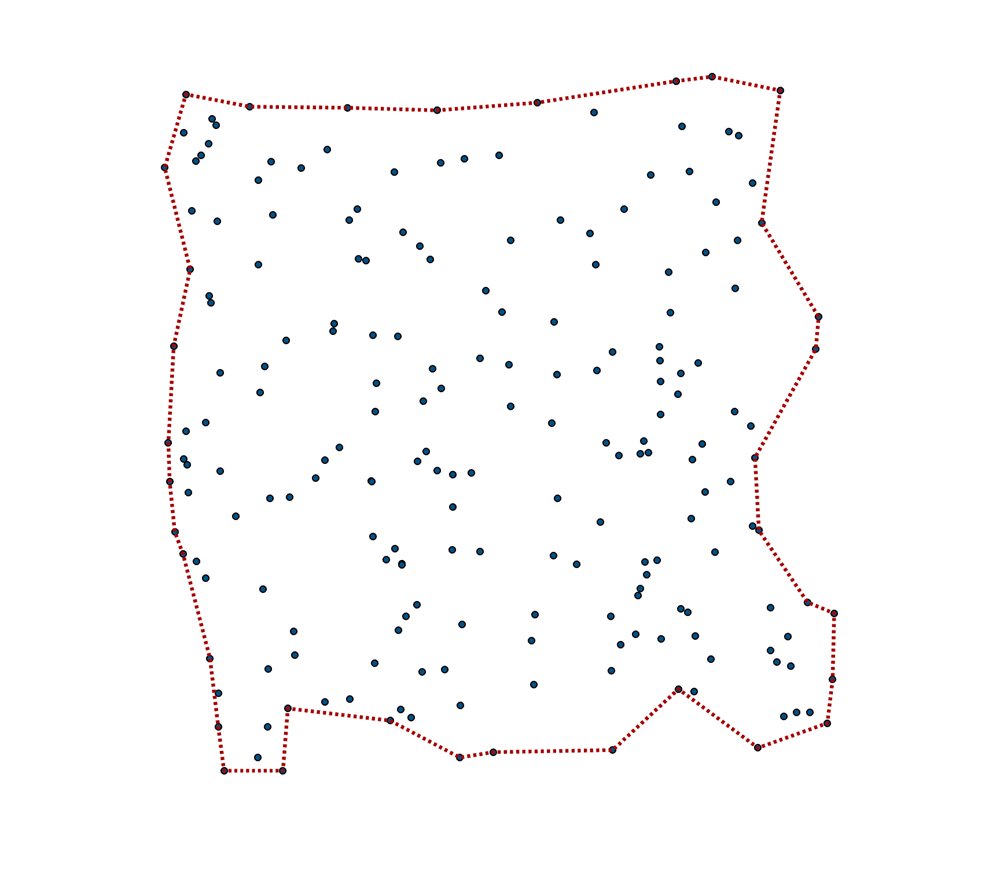
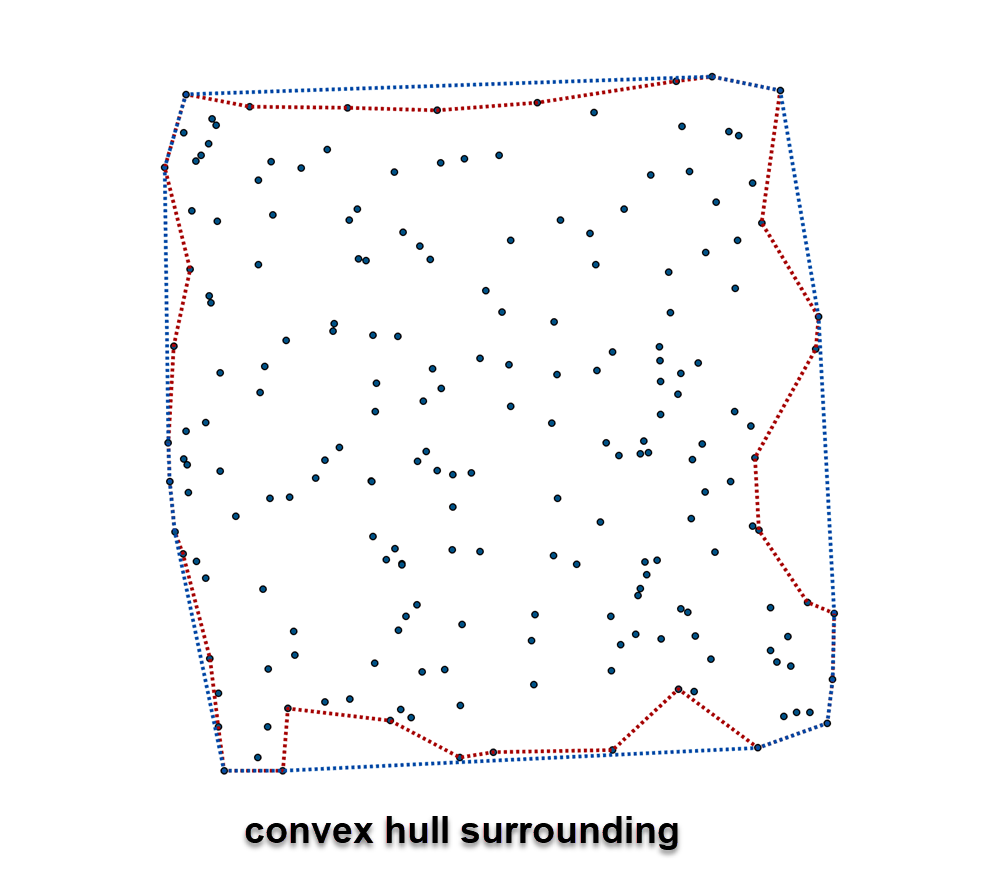
And finally... with the convex hull surrounding it.
And if that isn't tight enough for you, radial sorting and concave hull generation is as tight as it is going to get

So if you need to 'contain' something, add the concave hull to your suite of tools.
I will add the implementation of concave and convex hull to my