- Home
- :
- All Communities
- :
- Developers
- :
- Python
- :
- Python Questions
- :
- Arcpy.PointGeometry.pointFromAngleAndDistance help...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Arcpy.PointGeometry.pointFromAngleAndDistance help needed
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi All,
I won't say projections and transformation and all the math involved in coordinate systems are my strong point but something seems off when I use this method to create points at specified angles/distances - especially at the 0, 90, 180, 270 angles. It could just be my understanding of the math and potentially this method is not the correct tool for the job as they say. Here's my simple test and what I'm seeing:
Create a point in a projected coordinate system (Montana State Plane: 102300) at the center (0,0).
Use this method to create a new point with angle 0, distance 10,000 meters and the "PLANAR" option.
My exception (which could be wildly wrong) would be to get the point (0,10000). Since my angle is 0, i'm not expecting the X value to change --- at least when using the PLANAR option. The result i get is (954.9342, 9961.7461) ... so over 10,000 meters I've deviated 1,000 meters in the X and came up 40 meters short in the Y. Does this seem correct for the "PLANAR" option?
I was expecting pretty basic Cartesian math here... but maybe not? When I run the reverse method 'angleAndDistanceTo' using the two points, it DOES return 0 for angle and 10,000 for distance so it's at least being consistent in both directions.
However when I try any of the other options GEODESIC,GREAT_ELLIPTIC, LOXODROME, and PRESERVE_SHAPE I get the same point coordinates. Which sort of makes me think something is off with the function .... Shouldn't there be some differences with these options?
I get slightly different numbers if I choose a UTM zone rather than the MT SP system so the math appears to be using specifics of the coordinate system but again I wasn't expecting that for the "PLANAR" option. The help on the methods don't really shed much light on it either: PointGeometry—Help | ArcGIS for Desktop
TEST CODE
ptg = arcpy.PointGeometry(arcpy.Point(0,0), arcpy.SpatialReference(102300)) ptg.firstPoint ptg_1 = ptg.pointFromAngleAndDistance(0, 10000, "PLANAR") ptg_1.firstPoint ptg.angleAndDistanceTo(ptg_1, "PLANAR") ptg_1 = ptg.pointFromAngleAndDistance(0, 10000, "GEODESIC") ptg_1.firstPoint ptg_1 = ptg.pointFromAngleAndDistance(0, 10000, "GREAT_ELLIPTIC") ptg_1.firstPoint ptg_1 = ptg.pointFromAngleAndDistance(0, 10000, "LOXODROME") ptg_1.firstPoint ptg_1 = ptg.pointFromAngleAndDistance(0, 10000, "PRESERVE_SHAPE") ptg_1.firstPoint
RESULTS
<Point (0.0, 0.0, #, #)>
<Point (954.907914023, 9961.4713466, #, #)>
(0.0, 10000.000000000931)
<Point (954.907914023, 9961.4713466, #, #)>
<Point (954.907914023, 9961.4713466, #, #)>
<Point (954.907914023, 9961.4713466, #, #)>
<Point (954.907914023, 9961.4713466, #, #)>
The overall goal is to construct transects to a feature and even if the math is correct, the visual result is not what user expects which are exactly perpendicular lines thru the feature:

It's likely the math is correct and my understanding of the function is off so I need to simply write my own "planar" functions for this but that's not really obvious from the help.
Thanks for any enlightenment you like to share.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I am not familiar with that coordinate system, but is 0,0 the actual middle of the reference system? The only reason I question, is that in many projected coordinate systems, like UTM there is a false easting and false northing to the system (ie UTM 500,000m and 0 m to represent the center of the zone and 0 as the reference for the equator).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Yes, it does have a false easting. But why would that matter? I get the same deviations no matter what coordinate pair I choose. I picked 0,0 for the example so it's easy to see the result. If I pick (1234,5687) and use an angle of 0, I expect the X value to stay constant. It doesn't. I've run the code above with a number of different projected coordinate system IDs and get similar results. When I change to a geographic coordinate system (eg 4326) there's definitely differences between the results with different options.
>>> ptg = arcpy.PointGeometry(arcpy.Point(1234,5678), arcpy.SpatialReference(102300)) >>> ptg_1 = ptg.pointFromAngleAndDistance(0, 10000, "PLANAR") >>> ptg_1.firstPoint <Point (2187.77603462, 15639.1245447, #, #)>
The data generated in the picture above is UTM Zone 15N.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
If you want to try an example, pick the middle point for your latitude.
For example: -75.0 longitude, 45N latitude represents the middle(ish) of UTM zone 18 (my location-ish)
If I assign that point planar coordinates, then it would be (500,000m. 5,000,000m ) in terms of easting and northing (0k,0 isn't even within the zone, 0m is at the equator and 0m (easting is outside the zone to the west)
Try your projected origin point as 500,000, 5,000,000 then do your distance and angle calculations from that point and see what you get. Alternately, you could do -75, 45 (degrees long, lat) for distance and angles from a geographic location instead of a projected location.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Ok, Using UTM Zone 18N and the false easting the X value stays constant but the Y value is not exact but that matches the projection "scale" factor....
>>> ptg = arcpy.PointGeometry(arcpy.Point(500000,0), arcpy.SpatialReference(26918)) >>> ptg_1 = ptg.pointFromAngleAndDistance(0, 10000, "PLANAR") >>> ptg_1.firstPoint <Point (500000.0, 9996.0, #, #)>
So this function IS taking the projection into account AND NOT computing simple "planar" coordinates...X is not constant at an angle 0 everywhere in the coordinate plane (which seems off)
Also why is the result for the function with "PLANAR" the same as the result for "GEODESIC" ?
In the end, I'm trying to construct geometry in a similar fashion to the COGO editor which DOES understand the constant X --- see picture. I was expecting that the PLANAR option of these methods would allow for COGO type geometry construction but that doesn't appear to be the case.
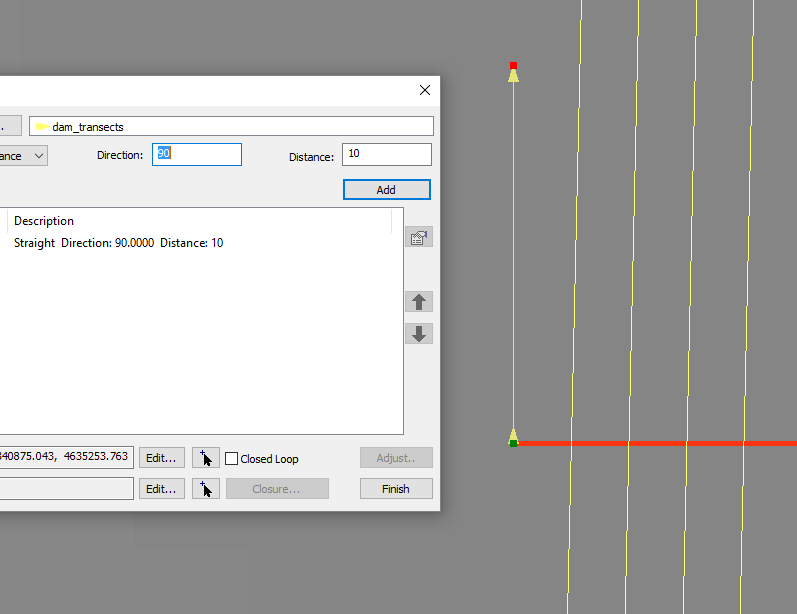
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Ok... you are working on the equator again (500,000,0) within UTM zone 18)
I hoped that you would try what you want to to calculate and do from your known point. my example suggested 500,000 and 5,000,000 which is the middle in any utm zone if you leave the zone number out.
When you get near the equator, things get flattish is both the x and y direction. Move north... you ultimately want to know what is going on in your area.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks, I did give it a try but didn't make a difference from the version I posted, see below ... I looked in the UTM definition and the false northing is 0 so I tried that pair as well. That's when I noticed the scale value was identical to Y deviation:
>>> ptg = arcpy.PointGeometry(arcpy.Point(500000,5000000), arcpy.SpatialReference(26918)) >>> ptg_1 = ptg.pointFromAngleAndDistance(0, 10000, "PLANAR") >>> ptg_1.firstPoint <Point (500000.0, 5009996.0, #, #)>

Anyway, this is all good, but doesn't really explain what this function is supposed to do and what the result of the different options should be....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Well
About geodetic features—Help | ArcGIS for Desktop
Creating geodetic features—Help | ArcGIS for Desktop
XY To Line—Help | ArcGIS for Desktop
Bearing Distance To Line—Help | ArcGIS for Desktop
is the order of logic and is generally only applicable to 'large' distances.
Since UTM is a conformal projection it is pretty good at retaining shape, area, distance and direction... but not perfect. There equi- projections (equidistance etc) but if working with small areas, distances etc, planar coordinates are suffice for most applications. As you found out, your distance for 10 km returned 9.996 km about a 4 part in 10,000 potential error, since the measure was at the central meridian, whih hass that scale factor. If you use a modified transverse mercator projection (state plane???) is based on a 3 degree lune rather than the 6 degree lune used by UTM. For MTM, the scale factor is 0.9999, the central meridian will be a different value and the false northing is the same-ish. The zone numbers aren't tied to utm, so don't even go there.
If you are trying to do survey grade positioning and measurements, then you would most likely keep your coordinates in decimal degrees, use an appropriate Earth model (datum) and calculate your measures using geodetic principles. You can then determine the distance between two points (great circles, meridians and the equator), along parallels (lines of latitude) and lines that represent constant bearing etc etc. I would consult a survey engineer for more current methodology. The last time I did field surveying was with a theodolite ... we used relative benchmarks... and the world was flat ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
If you pick a different angle than 0 degrees, you will see that "GEODESIC" results don't always match "PLANAR" results. That said, Esri does seem to be using a different definition of "PLANAR" than one expects when seeing the word. At a minimum, the software is working as designed and their documentation is inaccurate/incomplete. I would open an Esri Support incident.
Since 2D math is straightforward, or at least more so than 3D math, you could just role your own function. Prior to the release of ArcGIS 10.3 where pointFromAngleAndDistance was introduced, I presented a related function in the Calculating distance along a line from beginning to first intersection:
def linefromPolarCoord(angle, distance, point, spatialReference=None):
X = distance * math.cos(math.radians(90 - angle))
Y = distance * math.sin(math.radians(90 - angle))
return arcpy.Polyline(
arcpy.Array([point, arcpy.Point(point.X + X, point.Y + Y)]),
spatialReference
) The above function assumes basic 2D/projected data. The angle is degrees, distance is in units of the projection (meters for UTM), point is an arcpy.Point, and spatialReference is an arcpy.spatialReference for the projection being used.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Not sure if the OP opened a Support case or not, but I got a couple bugs logged:
#BUG-000095821 The arcpy method 'pointFromAngleAndDistance' returns the same coordinates regardless of whether the PLANAR or GEODESIC method is used.
#BUG-000095820 The arcpy method 'pointFromAngleAndDistance' returns an incorrect output geometry.
The former bug is still being assessed, but the latter one has been put in a product plan, although I can't say for sure which version.